Câu 1: 9.27 \(\le\)3n \(\le\)243
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
2
15 tháng 9 2019
a) \(2\cdot16\ge2^n>4\\ 2\cdot2^4\ge2^n>2^2\\ 2^5\ge2^n>2^2\\ \Rightarrow2^n\in\left\{2^3;2^4;2^5\right\}\\ \Rightarrow n\in\left\{3;4;5\right\}\)Vậy \(n\in\left\{3;4;5\right\}\)
b) \(9\cdot27\le3^n\le243\\ 3^2\cdot3^3\le3^n\le3^5\\ 3^5\le3^n\le3^5\\ \Rightarrow3^n=3^5\\ \Rightarrow n=5\)Vậy n = 5
VM
15 tháng 9 2019
a) \(2.16\ge2^n>4\)
\(\Rightarrow32\ge2^n>4\)
\(\Rightarrow2^5\ge2^n>2^2\)
\(\Rightarrow5\ge n>2\)
\(\Rightarrow\left\{{}\begin{matrix}n=3\\n=4\\n=5\end{matrix}\right.\)
Vậy \(n\in\left\{3;4;5\right\}.\)
b) \(9.27\le3^n\le243\)
\(\Rightarrow243\le3^n\le243\)
\(\Rightarrow3^5\le3^n\le3^5\)
\(\Rightarrow5\le n\le5\)
\(\Rightarrow n=5\)
Vậy \(n=5.\)
Chúc bạn học tốt!
3 tháng 10 2018
a) \(\frac{1}{9}\cdot27^n=3^n\)
\(\frac{1}{9}=\frac{3^n}{27^n}\)
\(\frac{1}{9}=\frac{3^n}{3^{3n}}\)
\(\frac{1}{9}=\frac{1}{3^{2n}}\)
=> 32n = 9 = 32
=> 2n = 2
=> n = 1
PT
1
VT
1
30 tháng 6 2015
1, 32 < 2^n < 128
2^5 < 2^n < 2^7
=> 5 < n < 7
Vì n là nguyên dương => n = 6
2, 2.16 > (=) 2^n > 4
2.2^4 > (=) 2^n > 2^2
2^5 > (=) 2^n > 2^2
5 >(=) n > 2 => n = 5 ; 4 ; 3
3, 9.27 < 3^n <= 243
3^2 . 3^3 < 3^n <= 3^5
3^5 < 3^n <=5
5 < n <= 5 ( không có n)
VM
29 tháng 10 2019
\(9.27\le\left(\frac{1}{3}\right)^x\le27.243\)
\(\Rightarrow243\le\left(\frac{1}{3}\right)^x\le6561\)
\(\Rightarrow\left(\frac{1}{3}\right)^{-5}\le\left(\frac{1}{3}\right)^x\le\left(\frac{1}{3}\right)^{-8}\)
\(\Rightarrow-5\le x\le-8\)
\(\Rightarrow\left\{{}\begin{matrix}x=-5\\x=-6\\x=-7\\x=-8\end{matrix}\right.\)
Vậy \(x\in\left\{-5;-6;-7;-8\right\}.\)
Chúc bạn học tốt!
VC
9
29 tháng 10 2019
\(9.27\le\left(\frac{1}{3}\right)^x\le27.243\)
\(243\le\left(\frac{1}{3}\right)^x\le6561\)
đến đây toi tịt ==
29 tháng 10 2019
à để xem !!! như thế này này :
\(3^5\le\left(\frac{1}{3}\right)^x\le3^8\)
Ta có \(\frac{1}{3}=0,\left(3\right)=\sqrt{3}=3\)( bt là số vô tỉ nx xem đã )
\(\Rightarrow3^5\le3^x\le3^8\)
\(\Rightarrow x=6;7\)
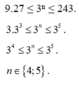
<=> 32.33 ≤ 3n ≤ 35
<=> 35 ≤ 3n ≤ 35
=> n = 5