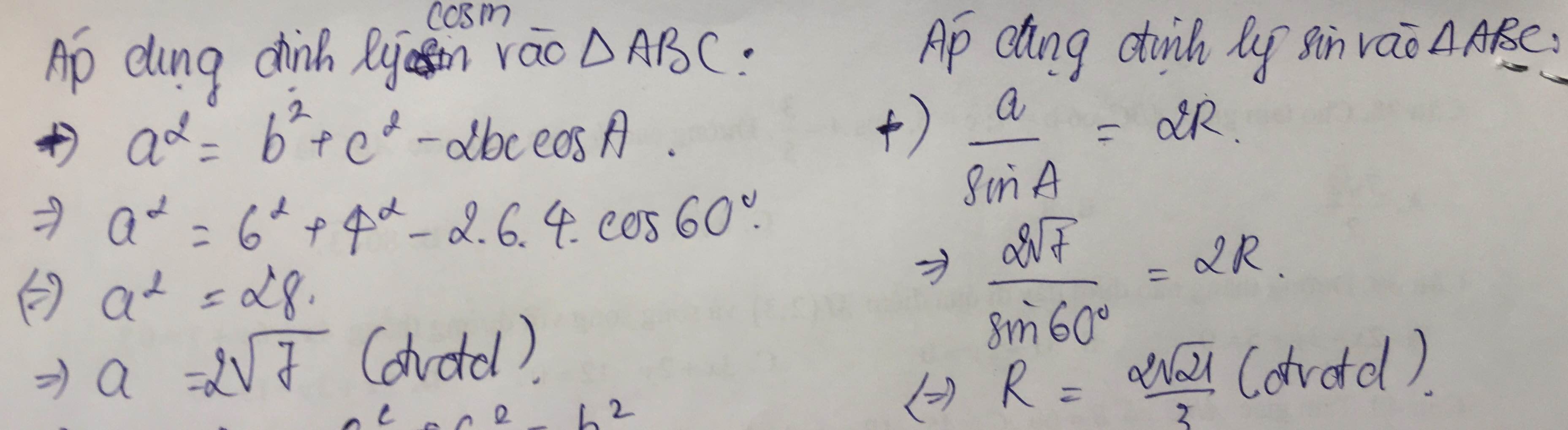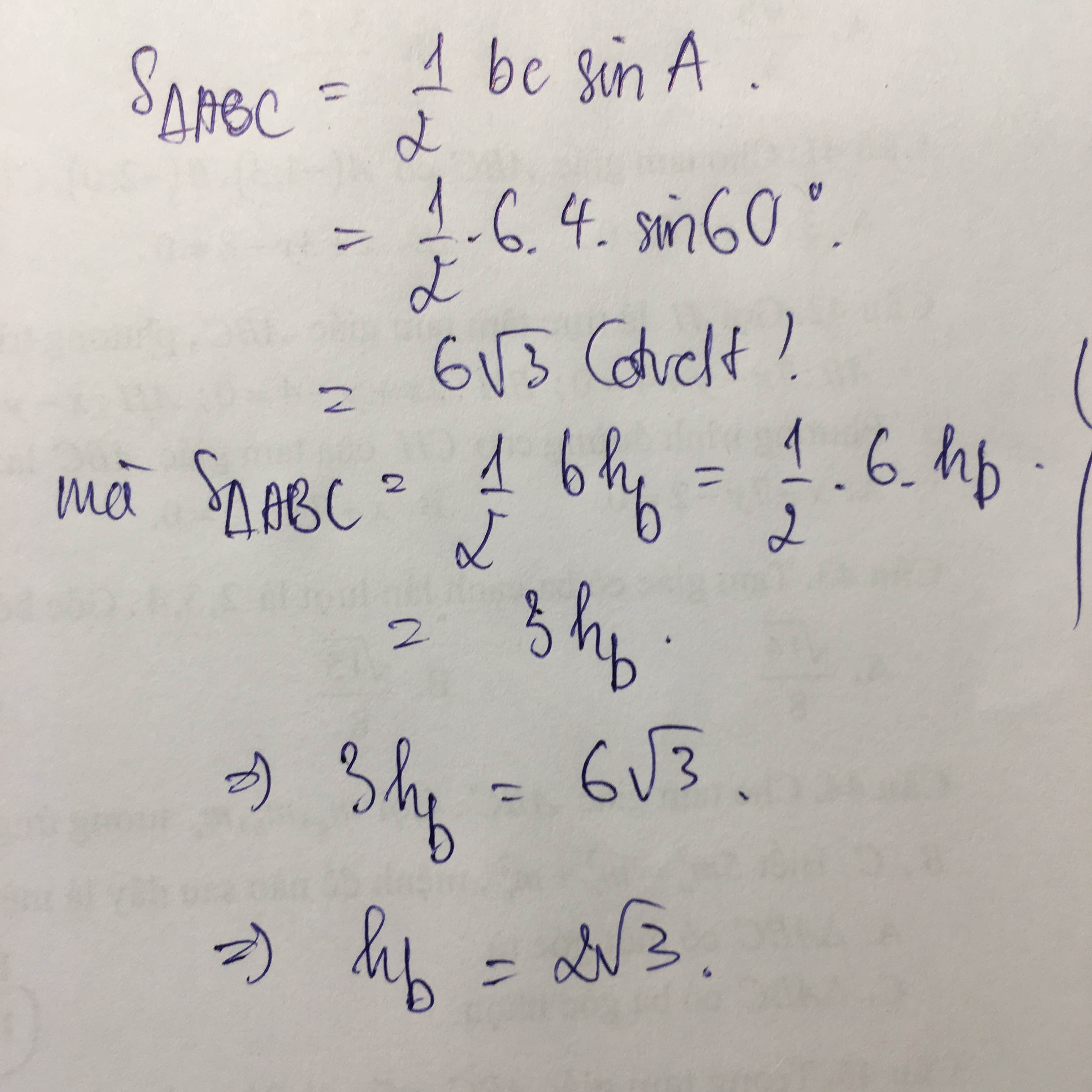Tam giác MNP cân tại M , cạnh bên = 6cm góc đỉnh bằng 120 độ. Tính bán kính đường tròn ngoại tiếp tam giác.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
12 tháng 4 2021
Lời giải:
Ta nhớ lại công thức, trong tam giác $ABC$ có $AB=c, BC=a, CA=b$ thì:
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$.
Ứng vào bài toán, với $\sin A=\sin 120=\frac{\sqrt{3}}{2}$ và $a=BC=6$ thì:
$R=\frac{a}{2\sin A}=\frac{6}{2.\frac{\sqrt{3}}{2}}=2\sqrt{3}$
CM
28 tháng 2 2018
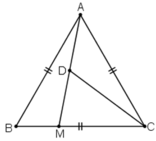
a) Do tam giác ABC là tam giác đều nên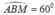 
.
Theo định lý côsin trong tam giác ABM ta có:
b) Theo định lý sin trong tam giác ABM ta có:
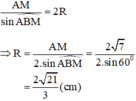
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
17 tháng 6 2019
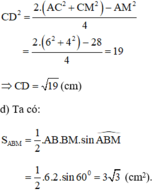
Gọi đường tròn (O; R) là đường tròn ngoại tiếp tam giác ABC.
Kẻ đường kính AO cắt (O) tại D.
Hai tam giác vuông ABH và ADC có ∠ABH =∠ADC (cùng chắn cung AC) nên chúng đồng dạng.
=>ABAD=AHAC=>ABAD=AHAC
=>AD=AB⋅ACAH=6⋅103=20(cm)=>AD=AB⋅ACAH=6⋅103=20(cm)
Do đó, R=AD2=202=10(cm)
P.s:Ko chắc
18 tháng 2 2017
Kẽ OA cắt đường tròn tại D cắt BC tại K
Ta có OA = OB = OD = R
\(\Rightarrow\)\(\Delta ABD\) vuông tại D
\(\Rightarrow BD=\sqrt{OD^2-AB^2}=\sqrt{10^2-8^2}=6\)
Ta có OK là đường trung trực của BC nên \(\hept{\begin{cases}OK⊥BC\\BK=CK\end{cases}}\)
Ta lại có: \(S_{\Delta ABD}=\frac{1}{2}AB.BD=\frac{1}{2}AD.BK\)
\(\Rightarrow BK=\frac{AB.BD}{AD}=\frac{8.6}{10}=4,8\)
\(\Rightarrow BC=2BK=4,8.2=9,6\)
18 tháng 2 2017
Viết nhầm tùm lum hết. Do không thấy cái hình. Mà thôi nhìn hình sửa hộ luôn nhé