Cho đường tròn (O)có hai đường kính AB, CD vuông góc với nhau. Gọi M là một điểm di động trên đoạn OB (M không thuộc O, B) . Tia CM cắt BD tại P và đường tròn tại N (N không thuộc C). Gọi Q là giao
điểm của AN và CD
a) Chứng minh tứ giác DQPN nội tiếp và PQ vuông góc với CD
b) Chứng minh tam giác ACQ đồng dạng tam giác CQN và diện tích tử giác ACMQ không đổi khi M thay đổi trên OB
c) Chứng minh tâm đường tròn ngoại tiếp tam giác CON luôn nằm trên một đường thẳng cố định khi M thay đổi trên OB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN//AC//BD

1. Ta có ÐOMP = 900 ( vì PM ^ AB ); ÐONP = 900 (vì NP là tiếp tuyến ).
Như vậy M và N cùng nhìn OP dưới một góc bằng 900 => M và N cùng nằm trên đường tròn đường kính OP => Tứ giác OMNP nội tiếp.
2. Tứ giác OMNP nội tiếp => ÐOPM = Ð ONM (nội tiếp chắn cung OM)
Tam giác ONC cân tại O vì có ON = OC = R => ÐONC = ÐOCN
=> ÐOPM = ÐOCM.
Xét hai tam giác OMC và MOP ta có ÐMOC = ÐOMP = 900; ÐOPM = ÐOCM => ÐCMO = ÐPOM lại có MO là cạnh chung => DOMC = DMOP => OC = MP. (1)
Theo giả thiết Ta có CD ^ AB; PM ^ AB => CO//PM (2).
Từ (1) và (2) => Tứ giác CMPO là hình bình hành.
3. Xét hai tam giác OMC và NDC ta có ÐMOC = 900 ( gt CD ^ AB); ÐDNC = 900 (nội tiếp chắn nửa đường tròn ) => ÐMOC =ÐDNC = 900 lại có ÐC là góc chung => DOMC ~DNDC
=> => CM. CN = CO.CD mà CO = R; CD = 2R nên CO.CD = 2R2 không đổi => CM.CN =2R2không đổi hay tích CM. CN không phụ thuộc vào vị trí của điểm M.
.

1) Xét (O) có
\(\widehat{ANB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{ANB}=90^0\)
Xét tứ giác ANMO có
\(\widehat{ANM}+\widehat{AOM}=180^0\left(90^0+90^0=180^0\right)\)
nên ANMO là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
2) Vì AB⊥CD(gt)
mà AB,CD là các đường kính của (O)
nên D là điểm chính giữa của cung AB
Xét (O) có
\(\widehat{AND}\) là góc nội tiếp chắn cung AD
\(\widehat{BND}\) là góc nội tiếp chắn cung BD
\(sđ\stackrel\frown{AD}=sđ\stackrel\frown{BD}\)(D là điểm chính giữa của cung AB)
Do đó: \(\widehat{AND}=\widehat{BND}\)(Hệ quả góc nội tiếp)
hay ND là tia phân giác của \(\widehat{ANB}\)(đpcm)

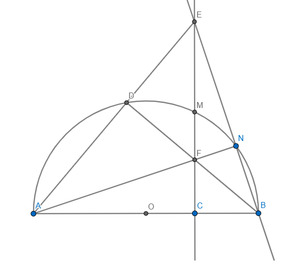
a) Vì AB là đường kính \(\Rightarrow\angle ANB=90\)
\(\Rightarrow\angle FNB+\angle FCB=90+90=180\Rightarrow BCFN\) nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Xét \(\Delta ACE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle ADB=\angle ACE=90\\\angle BAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AB}\Rightarrow AD.AE=AB.AC\)

a: góc BNA=1/2*180=90 độ
góc FNB+góc FCB=180 độ
=>FCBN nội tiếp
b: góc ADB=1/2*180=90 độ
Xét ΔADB vuông tạiD và ΔACE vuông tại C có
góc A chung
=>ΔADB đồng dạng với ΔACE
=>AD/AC=AB/AE
=>AC*AB=AD*AE
c: Xét ΔEAB có
EC,AN là đường cao
EC cắt AN tại F
=>F là trực tâm
=>BF vuông góc AE
mà BD vuông góc AE
nên B,F,D thẳng hàng

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA
a: sđ cung AC=sđ cung BC
=>góc ANC=góc BDC
=>góc PNQ=góc PDQ
=>DQPN nội tiếp
=>góc NQP=góc NDP
góc NDB=góc NAB
=>góc NQP=góc NAB
=>PQ//AB
=>PQ vuông góc CD
b: Xét ΔACQ và ΔMAC có
góc CAQ=góc AMC
góc AQC=góc MCA
=>ΔACQ đồng dạng với ΔMAC