Cho hình thang ABCD có AB//Cd. Trên AD lấy 2 điểm M và E sao cho AM=ME=ED. QUa M và E kẻ các đường thằng song song với AB cắt BC lần lượt tại N và F. Biết AB=12cm,EF=18cm. ĐỘ dài CD là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 9 2021
a:Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét ΔDAB có
M là trung điểm của AD
ME//AB
Do đó: E là trung điểm của BD
Xét ΔABC có
N là trung điểm của BC
NF//AB
Do đó: F là trung điểm của AC
24 tháng 10 2021
a: Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét ΔADC có
M là trung điểm của AD
MF//DC
Do đó: F là trung điểm của AC
Xét ΔBDC có
N là trung điểm của BC
NE//DC
Do đó: E là trung điểm của BD
CM
14 tháng 10 2019
Kẻ đường chéo AC cắt EF tại I
Trong ΔADC, ta có: EI // CD
Suy ra: 
Suy ra: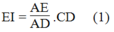 
Lại có :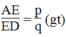 
Suy ra: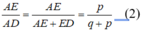 
Từ (1) và (2) suy ra: 
Trong ΔABC, ta có: FI // AB
Suy ra: 
(định lí ta-lét) (3)
Trong ΔADC, ta có : EI // CD
Suy ra: 
(định lí ta-lét) (4)
Từ (3) và (4) suy ra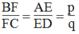 
Trong ΔABC, ta có: IF // AB
Suy ra: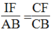 
(định lí ta-lét)
Suy ra: 
Ta có: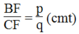 
Suy ra: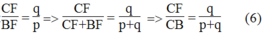 
Từ (5) và (6) suy ra: 
Vậy: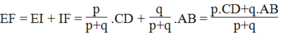 
Hình thang ABCD (AB//CD) có: M là trung điểm AE, MN//AB//EF.
\(\Rightarrow\)N là trung điểm BF nên MN là đường trung bình của hình thang ABCD.
\(\Rightarrow MN=\dfrac{AB+EF}{2}=\dfrac{12+18}{2}=15\left(cm\right)\).
Hình thang MNCD (MN//CD) có: E là trung điểm MD, EF//MN//CD.
\(\Rightarrow\)F là trung điểm CD nên EF là đường trung bình của hình thang MNCD.
\(\Rightarrow EF=\dfrac{MN+CD}{2}\Rightarrow CD=2EF-MN=2.18-15=21\left(cm\right)\)