cho
x4-x3+6x2-5x+3=(x2+ax+1)(x2+bx+3). Tìm a + b= ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DV
0
Những câu hỏi liên quan
CM
18 tháng 1 2017
a) Đây là phép chia ết với đa thức thương x 2 + 2x + 1.
Có thể kiểm tra lại kết quả bằng cách thực hiện nhân hai đa thức (x – 3)( x 2 + 2x +1)
b) Đa thức thương x 2 – 5.
17 tháng 9 2021
\(1,A⋮B\Leftrightarrow x^3-3x^2-ax+3=\left(x-1\right)\cdot a\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow1-3-a+3=0\\ \Leftrightarrow a=1\)
\(2,A⋮B\Leftrightarrow3x^3-16x^2+25x+a=\left(x^2-4x+3\right)\cdot b\left(x\right)\\ \Leftrightarrow3x^3-16x^2+25x+a=\left(x-3\right)\left(x-1\right)\cdot b\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow3-16+25+a=0\\ \Leftrightarrow a=-12\)
Thay \(x=3\)
\(\Leftrightarrow3\cdot27-16\cdot9+25\cdot3+a=0\\ \Leftrightarrow81-144+75+a=0\\ \Leftrightarrow12+a=0\Leftrightarrow a=-12\)
Vậy \(a=-12\)
8 tháng 1 2021
a) Ta có: \(x^3+x^2+x+1=0\)
\(\Leftrightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\)
mà \(x^2+1>0\forall x\)
nên x+1=0
hay x=-1
Vậy: S={-1}
b) Ta có: \(x^3-6x^2+11x-6=0\)
\(\Leftrightarrow x^3-x^2-5x^2+5x+6x-6=0\)
\(\Leftrightarrow x^2\left(x-1\right)-5x\left(x-1\right)+6\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-5x+6\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x-2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=3\end{matrix}\right.\)
Vậy: S={1;2;3}
c) Ta có: \(x^3-x^2-21x+45=0\)
\(\Leftrightarrow x^3-3x^2+2x^2-6x-15x+45=0\)
\(\Leftrightarrow x^2\left(x-3\right)+2x\left(x-3\right)-15\left(x-3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+2x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x^2+5x-3x-15\right)=0\)
\(\Leftrightarrow\left(x-3\right)^2\cdot\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)
Vậy: S={3;-5}
d) Ta có: \(x^4+2x^3-4x^2-5x-6=0\)
\(\Leftrightarrow x^4-2x^3+4x^3-8x^2+4x^2-8x+3x-6=0\)
\(\Leftrightarrow x^3\left(x-2\right)+4x^2\cdot\left(x-2\right)+4x\left(x-2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+4x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^3+3x^2+x^2+4x+3\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left[x^2\left(x+3\right)+\left(x+1\right)\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+3\right)\left(x^2+x+1\right)=0\)
mà \(x^2+x+1>0\forall x\)
nên (x-2)(x+3)=0
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-3\end{matrix}\right.\)
Vậy: S={2;-3}
28 tháng 6 2021
Chia nhỏ ra cậu ơi :v
Cậu đặt câu hỏi free nên đặt nhỏ ra thì mới có người làm nha để như này dày cộp không ai dám làm đou =(((
17 tháng 6 2016
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có
x1 + x2 + x3 + x4 ≥ 4
PT
1
CM
24 tháng 11 2018
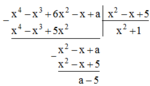
Để có phép chia hết thì số dư phải bằng 0.
Ta có: a – 5 = 0 hay a = 5.