Giải bài toán bằng cách lập phương trình
Một người chỉ định đi từ A đến B với vận tốc 48km/h. Nhưng đi được 1h thì bị tàu hỏa chắn ngang đường phải nghỉ 10 phút. Sau đó để đến B đúng giờ người đó phải tăng vận tốc lên 6km/h.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 8 2018
Đáp án C
* Phân tích:
Ta luôn có: Quãng đường = vận tốc . thời gian
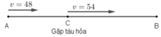
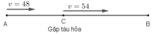
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h trong 1h nên SAC = 48km.
Xét trên quãng đường BC, để đến B đúng thời gian đã định ô tô đi với vận tốc 48 + 6 = 54 (km/h).
Vì ô tô đến B đúng thời gian đã định nên thời gian thực tế ô tô đi từ B đến C ít hơn thời gian dự định là 10 phút = 1/6 giờ (là thời gian chờ tàu hỏa).
| Quãng đường BC | Vận tốc | Thời gian | |
| Dự tính | x | 48 |  |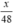
| Thực tế | x | 48 + 6 = 54 |  |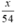
Ta có phương trình: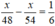 
* Giải:
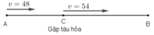
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h và đi trong 1 giờ
⇒ SAC = 48.1 = 48 (km).
Gọi quãng đường BC dài là x (km; x > 0).
Vận tốc dự tính đi trên BC là: 48 km/h
⇒ Thời gian dự tính đi quãng đường BC hết: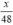 
(giờ).
Thực tế ô tô đi quãng đường BC với vận tốc bằng 48 + 6 = 54 (km/h).
⇒ Thời gian thực tế ô tô đi quãng đường BC là: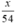 
(giờ).
Thời gian chênh nhau giữa dự tính và thực tế chính là thời gian ô tô đợi tàu hỏa là 10 phút = 1/6 (giờ).
Do đó ta có phương trình:
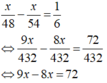
⇔ x = 72 (thỏa mãn) nên quãng đường BC là 72 (km).
Vậy quãng đường AB là:
SAB = SAC + SBC = 48 + 72 = 120 (km).
CM
3 tháng 9 2017
* Phân tích:
Ta luôn có: Quãng đường = vận tốc . thời gian
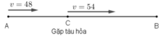
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h trong 1h nên SAC = 48km.
Xét trên quãng đường BC, để đến B đúng thời gian đã định ô tô đi với vận tốc 48 + 6 = 54 (km/h).
Vì ô tô đến B đúng thời gian đã định nên thời gian thực tế ô tô đi từ B đến C ít hơn thời gian dự định là 10 phút = 1/6 giờ (là thời gian chờ tàu hỏa).
| Quãng đường BC | Vận tốc | Thời gian | |
| Dự tính | x | 48 |  |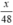
| Thực tế | x | 48 + 6 = 54 |  |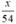
Ta có phương trình: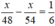 
* Giải:
Gọi C là địa điểm ô tô gặp tàu hỏa.
Quãng đường AC ô tô đi với vận tốc 48km/h và đi trong 1 giờ
⇒ SAC = 48.1 = 48 (km).
Gọi quãng đường BC dài là x (km; x > 0).
Vận tốc dự tính đi trên BC là: 48 km/h
⇒ Thời gian dự tính đi quãng đường BC hết: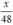 
(giờ).
Thực tế ô tô đi quãng đường BC với vận tốc bằng 48 + 6 = 54 (km/h).
⇒ Thời gian thực tế ô tô đi quãng đường BC là: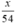 
(giờ).
Thời gian chênh nhau giữa dự tính và thực tế chính là thời gian ô tô đợi tàu hỏa là 10 phút = 1/6 (giờ).
Do đó ta có phương trình:
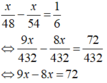
⇔ x = 72 (thỏa mãn) nên quãng đường BC là 72 (km).
Vậy quãng đường AB là:
SAB = SAC + SBC = 48 + 72 = 120 (km).
1 tháng 3 2015
Mình trình bày nè!
Gọi t là thời gian người đó đi từ A đến B
Ta có phương trình:
48t= 48+54(t-1-1/6)
Từ phương trình trên bạn sẽ tính được thời gian là 2.5(h).
Từ đó bạn sẽ dễ dàng tính được quãng đường AB bằng 120km
HT
4 tháng 8 2017
Giống câu hỏi của mk nhưng mk k bt làm ahiuhiu. Ban nào giúp mk vs
1 tháng 5 2018
Mình trình bày nè!
Gọi t là thời gian người đó đi từ A đến B
Ta có phương trình:
48t= 48+54(t-1-1/6)
Từ phương trình trên bạn sẽ tính được thời gian là 2.5(h).
Từ đó bạn sẽ dễ dàng tính được quãng đường AB bằng 120km
:3
26 tháng 2 2023
Gọi độ dài quãng đường AB là x
Thời gian dự kiến là x/48
Thời gian thực tế là 7/6+(x-48)/54
Theo đề, ta có: \(\dfrac{x-48}{54}+\dfrac{7}{6}=\dfrac{x}{48}\)
=>8(x-48)+7*72=9x
=>8x-384+504-9x=0
=>x=120
TG
26 tháng 2 2021
Đổi 10 p = \(\dfrac{1}{6}h\)
Gọi x (km) là độ dài quãng đường AB (x > 0)
Đoạn đường đi trong 1 h đầu là 48 km
Đoạn đường còn lại là x - 48 (km)
Thời gian dự định đi từ điểm bị tàu hỏa chắn đường đến B là: \(t_1=\dfrac{x-48}{48}\) (h)
Thời gian thực tê đi từ điểm bị tàu hỏa chắn đường đến B là \(t_2=\dfrac{x-48}{48+6}=\dfrac{x-48}{54}\) (h)
Vì ô tô bị tàu hỏa chắn đường trong 10p nên:
\(\dfrac{x-48}{48}-\dfrac{x-48}{54}=\dfrac{1}{6}\) (1)
Giải PT (1) <=> x = 120 (t/m ĐK)
Vậy quảng đường AB dài 120
P/s: Ko chắc nha
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
Bài 1:
Đổi 10 phút thành 1/6 giờ
Thời gian đi dự định: $\frac{AB}{48}$ (h)
Thời gian đi thực tế: $1+\frac{1}{6}+\frac{AB-48}{48+6}$
$=\frac{7}{6}+\frac{AB-48}{54}$ (h)
Ta có: $\frac{AB}{48}=\frac{7}{6}+\frac{AB-48}{54}$
$\Leftrightarrow \frac{AB}{432}=\frac{5}{18}$
$\Rightarrow AB=120$ (km)
AH
Akai Haruma
Giáo viên
13 tháng 8 2021
Bài 2:
Đổi 1h40 phút thành $\frac{5}{3}$ giờ, đổi 20 phút thành $\frac{1}{3}$ giờ
Thời gian dự định đi: $\frac{AB}{12}$ (giờ)
Thời gian thực tế: \(\frac{AB}{3.12}+\frac{1}{3}+\frac{2AB}{3.36}=\frac{5AB}{108}+\frac{1}{3}\) (giờ)
Theo bài ra:
$\frac{5AB}{108}+\frac{1}{3}+\frac{5}{3}=\frac{AB}{12}$
$\Leftrightarrow AB=54$ (km)
đề thiếu
tính quãng đường AB nữa nha