1 bông hoa giấy có kích thước như hình vẽ hỏi diện tích bông hoa là bao nhiêu cm2 biết mỗi cánh hoa đều là nửa hình tròn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 8 2023
Để tính diện tích bông hoa, ta cần biết diện tích của một nửa hình tròn.
Gọi cạnh hình vuông là a. Diện tích hình vuông ABCD là a^2 = 400 cm^2.
Vậy a = √400 = 20 cm.
Đường kính của nửa hình tròn là cạnh hình vuông, nên đường kính của nửa hình tròn là 20 cm.
Bán kính của nửa hình tròn là đường kính chia 2, nên bán kính của nửa hình tròn là 20/2 = 10 cm.
Diện tích của một nửa hình tròn là (1/2)πr^2, với r là bán kính.
Diện tích của một nửa hình tròn là (1/2)π(10 cm)^2 = 50π cm^2.
Vì bông hoa có 4 cánh, nên diện tích bông hoa là 4 lần diện tích của một nửa hình tròn.
Diện tích bông hoa là 4 x 50π cm^2 = 200π cm^2.
Kết quả cuối cùng là diện tích bông hoa là 200π cm^2.
TH
Thầy Hùng Olm
Manager
VIP
18 tháng 5 2023
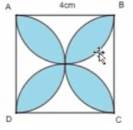
Diện tích hình vuông là:
6× 6 = 36 (cm²)
Diện tích 4 nửa hình tròn (2 hình tròn) là:
3x3x3,14 × 2 = 56,52 (cm²)
Diện tích hình bông hoa là:
36 + 56,52 = 92,52 (cm²)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 5 2023
Theo bài ra ta có hình vẽ minh họa như sau:
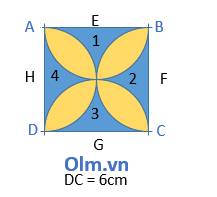
E; F; G; H lần lượt là trung điểm của các cạnh AB; BC; CD; DA
Bán kính của nửa hình tròn là 3 cm nên cạnh hình vuông ABCD là:
3 \(\times\) 2 = 6 (cm)
Diện tích hình vuông là: 6 \(\times\) 6 = 36 (cm2)
Diện tích mỗi nửa hình tròn có đường kính là cạnh hình vuông là:
3 \(\times\) 3 \(\times\) 3,14 : 2 = 14,13 (cm2)
Diện tích của hình bông hoa bốn cánh chính là phần diện tích của các hình được tô bởi màu vàng.
Diện tích của các hình được tô bởi màu vàng bằng diện tích hình vuông trừ đi tổng diện tích các hình được tô bởi màu xanh.
Gọi diện tích các hình được tô bởi màu xanh lần lượt là 1; 2; 3; 4 ta có:
S1 = S2 = S3 = S4 ⇒ S1 + S2 + S3 + S4 = (S1 + S3) \(\times\) 2
S1 + S3 = SABCD - \(\dfrac{1}{2}\)S(H;3cm) - \(\dfrac{1}{2}\)S(F;3cm)
S1 + S3 = 36 - 14,13 - 14,13 = 7,74 (cm2)
S1 + S2 + S3 + S4 = 7,74 \(\times\) 2 = 15,48 (cm2)
Diện tích của hình bông hoa 4 cánh bằng :
SABCD - ( S1 + S2 + S3 + S4)
36 - 15,48 = 20,52 (cm2)
Đáp số: 20,52 cm2
có ai ko giúp mi giải bài này