Cho △ABC ⊥Tại A có AB=5cm,AC=12cm
a/Tính BC
b/Trên tia đối của tia AB lấy điểm D sao cho AD=AB.C/M△ABC=△ADC
C/ Đường thẳng đi qua A //với BC cắt AD tai E.c/m △EAC cân
d/Gọi F là trung điểm của BC.CMG/CA,DF,BE đồng quy tai 1 điểm...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
24 tháng 4 2022
a).
Áp dụng đl pytago vào tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2=3^2+4^2\Rightarrow BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
So sánh góc:
\(\widehat{C}< \widehat{B}< \widehat{A}\)
b) . Xét 2 t/g vuông : ABC và ADC có :
\(\widehat{CAB}=\widehat{CAD}=90^o\)
AC cạnh chung
\(AB=AD\left(theođề\right)\)
do đó : t/g ABC = t/g ADC ( cạnh góc vuông - cạnh góc vuông).
c) . Vì t/g ABC = t/g ADC
=> \(\widehat{BCA}=\widehat{DCA}\left(1\right)\)
Vì AM // BC
= > \(\widehat{CAM}=\widehat{BCA}\left(soletrong\right)\left(2\right)\)
Từ (1) và (2)
=> \(\widehat{DCA}=\widehat{CAM}\) ( 2 góc đều = góc BCA ) .
=> tam giác AMC cân ( 2 góc đáy bằng nhau).
d) . Từ đề ta suy ra :
G là trực tâm của t/g CBD
=> \(CG=\dfrac{2}{3}AC=\dfrac{2}{3}.4=2,67\left(cm\right)\)
NA
1 tháng 5 2022
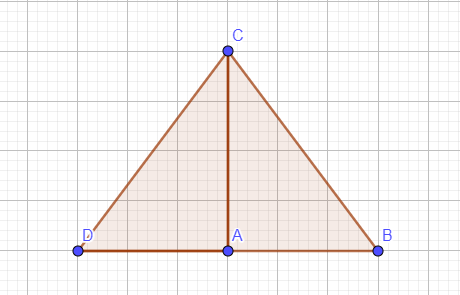
`a)` Áp dụng định lý pytago ta có :
`AB^2+AC^2=BC^2`
hay `9^2+12^2=BC^2`
`=>BC^2=225`
`=>BC=15(cm)`
`b)` Xét `ΔABC` và `ΔADC` ta có :
`AC` chung
`\hat{BAC}=90^o`
`\hat{DAC}=90^o`
`=>ΔABC=ΔADC` (c.g.c)
14 tháng 3 2022
a: BC=13cm
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD
Do đó: ΔABC=ΔADC
29 tháng 4 2018
a) Áp dụng định lý Py-ta-go, ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=5^2+12^2\)
\(\Rightarrow BC^2=169\left(cm\right)\)
\(\Rightarrow BC=\sqrt{169}=13\left(cm\right)\)
b) Vì \(\Delta ABC=\Delta ADC\)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\left(2\text{ góc tương ứng}\right)\)
Vì BC // AE (gt)
\(\Rightarrow\widehat{CED}=\widehat{C_1}\left(\text{so le}\right)\)
\(\Rightarrow\Delta EAC\text{ là tam giác cân. }\)
=> ĐPCM
d) Ta có: BF = CF (F là trung điểm của BC)
AB = AD (gt)
=> DP và AB là 2 đường trung tuyến của tam giác BDC
=> G là trọng điểm của tam giác BDC
=> BG là đường trung tuyến còn lại của tam giác BDC
<=> CA; DF; BE cùng đi qua 1 điểm hoặc CA; DF; BE đồng quy tại 1 điểm
=> ĐPCM
P/s: Mk vẽ hình hơi xấu, mong bn thông cảm
QN
16 tháng 3 2022
a) Áp dụng định lý Py-ta-go vào ∆ABC, ta được:
BC2=AB2+AC2
⟹BC2=52+122=169
⟹BC=13
Vậy BC=13cm
b)Xét ∆ ABM và ∆CEm,có
BM=MC(GT)
AM=ME(GT)
<BMA=<EMC( đối đỉnh)
⟹∆ ABM=∆CEM(c.g.c)
⟹ AB=EC(2 cạnh tương ứng)
⟹BC=AE(do BM=1/2BC(GT); EM=1/2AE(GT) mà BM=EM)
Xét ∆ABC và ∆CEA,ta có:
AB=EC(CMT)
AC cạnh chung
BC=AE(CMT)
⟹ ∆ABC=∆CEA(c.c.c)
⟹<A=<E ( 2 góc tương ứng)
⟹EC⊥ AC; AB⊥ AC⟹AB//EC( quan hệ từ vuông góc đến song song)
LD
31 tháng 3 2021
a) Áp dụng định lý Py-ta-go cho \(\Delta\)vuông ABC có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+12^2}=13\left(cm\right)\)
b) Xét \(\Delta ABC\)và \(\Delta ADC\)có:
\(\hept{\begin{cases}AB=AD\left(gt\right)\\gócBAC=gócDAC\left(=90^0\right)\\AC:chung\end{cases}}\)
\(\Rightarrow\Delta ABC=\Delta ADC\left(c.g.c\right)-\left(đpcm\right)\)
c) Xét \(\Delta BDC\)có: \(\hept{\begin{cases}\text{A là trung điểm BD}\\AE//BC\left(gt\right)\end{cases}}\)
\(\Rightarrow\text{E là trung điểm CD}\left(t/c\right)\)
Xét \(\Delta ADC\)vuông tại A có AE là đường trung tuyến ứng cạnh DC
\(\Rightarrow AE=\frac{1}{2}CD\left(t/c\right)=EC\left(\text{E là trung điểm CD}\right)\)
\(\Rightarrow\Delta AEC\)cân tại E (đpcm)
d) Gọi giao của AC và BE là O
Xét \(\Delta DBC\)có:\(\hept{\begin{cases}\text{BE là đường trung tuyến ứng cạnh CD }\left(gt\right)\\\text{CA là đường trung tuyến ứng cạnh BD }\left(gt\right)\end{cases}}\)
\(\Rightarrow\)O là trọng tâm của \(\Delta DBC\)
Mà DF là đường trung tuyến ứng cạnh BC
\(\Rightarrow\)CA, DF, BE cùng đồng quy tại 1 điểm (đpcm)
14 tháng 2 2018
D) cách 2:
Xét∆BDC có: BA=AD
BM=MC
=) AM là đường trung bình của∆BCD
=) AM//DC
Mà: AE//MC ( gt )
Suy ra: * EC=AM. (1)
( t/c đường chắn)
* AE=MC . (2)
Lại có: ∆AEC cân tại E=) AE=EC (3)
Từ (1);(2);(3)=) AM = MC
Mà M là trung điểm BC=) MC=1/2BC
Suy ra AM=1/2BC
b) Xét ΔABC vuông tại A và ΔADC vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔABC=ΔADC(hai cạnh góc vuông)
a) Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13(cm)
Vậy: BC=13cm