Tìm GTNN của A = x4 + 4x3 + 10x2 + 12x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
Lời giải:
$A=x^4-4x^3+7x^2-12x+75$
$=(x^2-2x)^2+3x^2-12x+75$
$=(x^2-2x)^2+3(x^2-4x+4)+63$
$=(x^2-2x)^2+3(x-2)^2+63\geq 63$
Vậy $A_{\min}=63$. Giá trị này đạt tại $x^2-2x=x-2=0$
$\Leftrightarrow x=2$
NK
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2021
\(A=\left(x^4-4x^3+4x^2\right)+\left(3x^2-12x+12\right)+63\)
\(A=x^2\left(x^2-4x+4\right)+3\left(x^2-4x+4\right)+63\)
\(A=\left(x^2+3\right)\left(x-2\right)^2+63\ge63\)
\(A_{min}=63\) khi \(x=2\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
a.
\(x^3-7x+6=0\)
\(\Leftrightarrow x^3-3x^2+2x+3x^2-9x+6=0\)
\(\Leftrightarrow x\left(x^2-3x+2\right)+3\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x^2-x-2x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-2\left(x-1\right)\right]\left(x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-3\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
f.
\(x^4-4x^3+12x-9=0\)
\(\Leftrightarrow x^4-4x^3+3x^2-3x^2+12x-9=0\)
\(\Leftrightarrow x^2\left(x^2-4x+3\right)-3\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow\left(x^2-4x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x^2-x-3x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-3\left(x-1\right)\right]\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x^2-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\\x=\pm\sqrt{3}\end{matrix}\right.\)
DT
18 tháng 2 2022
a, \(\Leftrightarrow\left(9x^2-4\right)\left(x+1\right)-\left(3x+2\right)\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(\left(9x^2-4\right)-\left(\left(3x+2\right)\left(x-1\right)\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-\left(3x^2-x-2\right)\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(9x^2-4-3x^2+x+2\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x^2+x-2\right)=0\)
\(\Leftrightarrow\left(x+1\right)=0;3x^2+x-2=0\)
=> x=-1
với \(3x^2+x-2=0\)
ta sử dụng công thức bậc 2 suy ra : \(x=\dfrac{2}{3};x=-1\)
Vậy ghiệm của pt trên \(S\in\left\{-1;\dfrac{2}{3}\right\}\)
18 tháng 2 2022
b: \(\Leftrightarrow x^2-2x+1-1+x^2=x+3-x^2-3x\)
\(\Leftrightarrow2x^2-2x=-x^2-2x+3\)
\(\Leftrightarrow3x^2=3\)
hay \(x\in\left\{1;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x+2\right)\left(x-3\right)-\left(x-1\right)\left(x-2\right)\left(x+2\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left[\left(x+1\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(x^2-2x-3-x^2-3x+10\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)\left(-5x+7\right)=0\)
hay \(x\in\left\{1;-2;\dfrac{7}{5}\right\}\)
HH
0
CM
7 tháng 5 2017
a) P xác định khi x3 – 4x ≠ 0
Ta có: x3 – 4x = x(x2 – 4)= x(x - 2)(x + 2) ≠ 0
⇒ x ≠ 0 và x ≠ 2 và x ≠ -2
PT
1
CM
10 tháng 12 2019
Đáp án A.
y = x4 + 4x3 TXĐ: D = R
y’ = 4x3 + 12x2 = 0 
Lập bảng xét dấu của y’ và suy ra hàm số có 1 cực trị
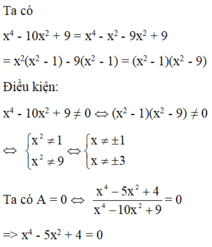
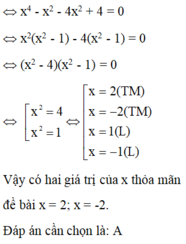
\(A=x^4+4x^3+10x^2+12x=x^4+4x^2+9+4x^3+12x+6x^2-9\)
<=>\(A=x^4+4x^2+9+4x^3+12x+6x^2-9\)
<=>\(A=\left(x^2\right)^2+\left(2x\right)^2+3^2+2.x^2.2x+2.2x.3+2.x^2.3-9\)
<=>\(A=\left(x^2+2x+3\right)^2-9\)
<=>\(A=\left[\left(x+1\right)^2+2\right]^2-9\)
Vì \(\left(x+1\right)^2\ge0\Leftrightarrow\left(x+1\right)^2+2\ge2\Leftrightarrow\left[\left(x+1\right)^2+2\right]^2\ge4\)\(\Leftrightarrow A=\left[\left(x+1\right)^2+2\right]^2-9\ge-5\)
=>Amin=-5 <=> x=-1
Vậy Amin=5 tại x=-1
\(\frac{x}{3}=\frac{y}{4}\)
\(\Rightarrow4x=3y\)
\(\Rightarrow\frac{x}{y}=\frac{3}{4}\)
\(\Rightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}y=4\\y=-4\end{cases}}\)