Cho tam giác ABC cân tại A, góc A nhọn. Đường cao BD và CE cắt nhau tại I
a) Chứng minh tam giác ABD bằng tam giác ACE
b) Chứng minh AI là tia phân giác của góc CAB
c) Chứng minh 2IB > BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MP
31 tháng 3 2018
a)Xét tam giác ABD và tam giác ACE,ta có:
A là góc chung
AB=AC(ví tam giác ABC cân tại A)
AE=AD(gt)
=> tam giác ABD=tam giác ACE(c.g.c)=>BD=CE( 2 cạnh tương ứng)
b)Vì BD,CE lần lượt là đường trung tuyến mà lại giao nhau tại G(mà BD=CE)=>GE=GD=1/3 BD=1/3 CE
=>EG=GD
Xét tam giác AEG và tam giác ADG ,ta có:
GE=GD(c/m trên)
AE=AD(gt)
AG cạnh chung
=>tam giác AEG=tam giác ADG(c.c.c)
=>góc EAG=góc DAG=>AG là tia p/g góc A
c)Ta có: Vì K là trung điểm AG;I là trung điểm GC và AD=DC
=>AI;CK:GD lần lượt là đường trung tuyến tam giác AGC=>BD;CK;AI đồng quy(t/c 3 đường trung tuyến của tam giác)
KV
5 tháng 1
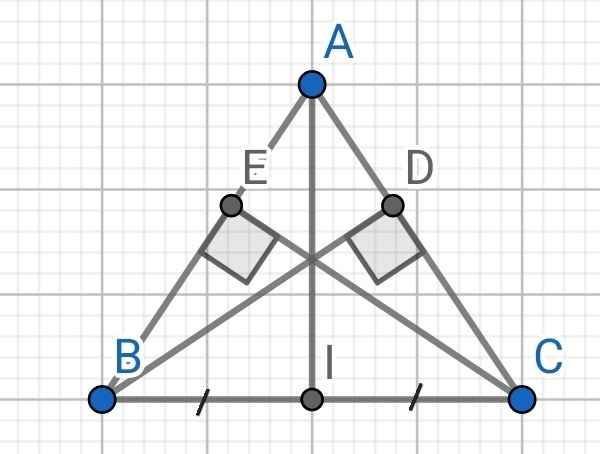a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
AB = AC (do ∆ABC cân tại A)
∠A chung
⇒ ∆ABD = ∆ACE (cạnh huyền - góc nhọn)
b) Do I là trung điểm của BC (gt)
⇒ IB = IC
Xét ∆ABI và ∆ACI có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆ABI = ∆ACI (c-c-c)
⇒ ∠BAI = ∠CAI (hai góc tương ứng)
⇒ AI là tia phân giác của ∠BAC
c) Do ∆ABI = ∆ACI (cmt)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
Mà ∠AIB + ∠AIC = 180⁰ (kề bù)
⇒ ∠AIB = ∠AIC = 180⁰ : 2 = 90⁰
⇒ AI ⊥ BC
BF
7 tháng 5 2017
Bạn tự vẽ hình ik nha
a. Xét tam giác ABD và tam giác ACE có:
góc D = góc E = 90* (gt)
AB = AC (gt)
góc A chung
=> tg ABD = tg ACE (c. huyền-g. nhọn)
b. Vì H là giao điểm của 2 dường cao BD và CE
Nên AH cũng là đường cao cùa tg ABC hay AH vuông góc BC
Do tg ABC là tam giác cân => AI là đường cao đồng thời cũng là dường trung tuyến => BI = CI => I là trung điểm của BC
c.Ta có: góc ACE = góc ABD (doc tg ABD = tg ACE)
và góc ABC = góc ACB
=> góc DBC = góc ECB
Ta có: BD vuông góc AC (gt)
CF vuông góc AC (gt)
=> CF song song BD (2 dường thẳng cùng vuông góc với 1 dường thẳng)
=> góc DBC = góc BCF ( so le trong)
Mà góc DBC = góc ECB
=> góc ECB = góc BCF
=> BC lá tia phân giác của góc ECF