a2 + b2 + c2 + 42=2a +8b +10c . khi đó a+b+c =?
- nêu cách giải giúp mình với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án D

Bài toán trở thành: Tìm M nằm trên đường tròn giao tuyến của mặt cầu (S) và mặt phẳng (P) sao cho KM lớn nhất







c: Ta có: \(a\left(a+2b\right)^3-b\left(2a+b\right)^3\)
\(=a^4+6a^3b+12a^2b^2+8ab^3-8a^3b-12a^2b^2-6ab^3-b^4\)
\(=a^4-2a^3b+2ab^3-b^4\)
\(=\left(a-b\right)\left(a+b\right)\left(a^2+b^2\right)-2ab\left(a^2-b^2\right)\)
\(=\left(a-b\right)^3\cdot\left(a+b\right)\)

Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
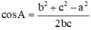
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.

ta có : \(a^2+b^2+c^2+42=2a+8b+10c\)
\(\Leftrightarrow\) \(a^2+b^2+c^2+42-2a-8b-10c=0\)
\(\Leftrightarrow\) \(\left(a^2-2a+1\right)+\left(b^2-8b+16\right)+\left(c^2-10c+25\right)=0\)
\(\Leftrightarrow\) \(\left(a-1\right)^2+\left(b-4\right)^2+\left(c-5\right)^2=0\)
mà \(\left\{{}\begin{matrix}\left(a-1\right)^2\ge0\forall a\\\left(b-4\right)^2\ge0\forall b\\\left(c-5\right)^2\ge0\forall c\end{matrix}\right.\)
\(\Rightarrow\) \(\left(a-1\right)^2+\left(b-4\right)^2+\left(c-5\right)^2=0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}\left(a-1\right)^2=0\\\left(b-4\right)^2=0\\\left(c-5\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}a-1=0\\b-4=0\\c-5=0\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}a=1\\b=4\\c=5\end{matrix}\right.\)
khi đó \(a+b+c=1+4+5=10\)

a: \(\Leftrightarrow a^2-4a+4+b^2-6b+9+c^2-2c+1>=0\)
\(\Leftrightarrow\left(a-2\right)^2+\left(b-3\right)^2+\left(c-1\right)^2>=0\)
Dấu '=' xảy ra (a,b,c)=(2;3;1)

Từ giả thiết:
\(a^2=2\left(b^2+c^2\right)\ge\left(b+c\right)^2\Rightarrow\left(\dfrac{a}{b+c}\right)^2\ge1\Rightarrow\dfrac{a}{b+c}\ge1\)
\(P=\dfrac{a}{b+c}+\dfrac{b^2}{bc+ab}+\dfrac{c^2}{ac+bc}\ge\dfrac{a}{b+c}+\dfrac{\left(b+c\right)^2}{a\left(b+c\right)+2bc}\ge\dfrac{a}{b+c}+\dfrac{\left(b+c\right)^2}{a\left(b+c\right)+\dfrac{1}{2}\left(b+c\right)^2}\)
\(P\ge\dfrac{a}{b+c}+\dfrac{1}{\dfrac{a}{b+c}+\dfrac{1}{2}}\)
Đặt \(\dfrac{a}{b+c}=x\ge1\)
\(\Rightarrow P\ge x+\dfrac{1}{x+\dfrac{1}{2}}=\dfrac{4}{9}\left(x+\dfrac{1}{2}\right)+\dfrac{1}{x+\dfrac{1}{2}}+\dfrac{5}{9}x-\dfrac{2}{9}\)
\(P\ge2\sqrt{\dfrac{4}{9}\left(x+\dfrac{1}{2}\right).\dfrac{1}{\left(x+\dfrac{1}{2}\right)}}+\dfrac{5}{9}.1-\dfrac{2}{9}=\dfrac{5}{3}\)
\(P_{min}=\dfrac{5}{3}\) khi \(x=1\) hay \(a=2b=2c\)
a2 + b2 + c2 + 42=2a +8b +10c
\(\Rightarrow a^2+b^2+c^2+42-2a-8b-10c=0\)
\(\Rightarrow\left(a^2-2a+1\right)+\left(b^2-8b+16\right)+\left(c^2-10c+25\right)=0\)
\(\Rightarrow\left(a-1\right)^2+\left(b-4\right)^2+\left(c-5\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}a-1=0\\b-4=0\\c-5=0\end{cases}}\Rightarrow\hept{\begin{cases}a=1\\b=4\\c=5\end{cases}}\)
Khi đó \(a+b+c=1+4+5=10\)
cho x<0 thỏa mãn \(\frac{1}{x^2+9x+20}\)+\(\frac{1}{x^2+11x+30}\)+\(\frac{1}{x^2+13x+42}\)=\(\frac{1}{18}\) tìm x=?
mn giải giúp mk với