các bạn cho mình hỏi cách tìm GTNN và GTLN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+1 còn tùy vào từng loại cần tìm nếu đơn giản là đa thức bậc 2 thì sử dụng máy tính hoặc cứ tìm thôi ;-;
+2 Vì \(m^2+3\ge3\) thì để dấu = xảy ra tức là : \(m^2+3=3\) \(\Leftrightarrow m^2=0\)
<=> m = 0 .

ta có \(x\in\left[-\frac{\pi}{4};0\right]\Rightarrow2x\in\left[-\frac{\pi}{2},0\right]\Rightarrow sin2x\in\left[-1,0\right]\)
Vậy \(\hept{\begin{cases}GTNN=-1\\GTLN=0\end{cases}}\)

a.
\(f'\left(x\right)=2cos2x-1=0\Rightarrow cos2x=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=-\dfrac{\pi}{6}\end{matrix}\right.\)
Ta có:
\(f\left(-\dfrac{\pi}{2}\right)=0+\dfrac{\pi}{2}=\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{2}\right)=0-\dfrac{\pi}{2}=-\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}-\dfrac{\pi}{6}\)
\(f\left(-\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{3}}{2}+\dfrac{\pi}{6}\)
So sánh các giá trị trên ta được:
\(f\left(x\right)_{max}=f\left(-\dfrac{\pi}{2}\right)=\dfrac{\pi}{2}\)
\(f\left(x\right)_{min}=f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}\)
b.
\(f'\left(x\right)=3-2\sqrt{3}sin2x=0\Rightarrow sin2x=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=\dfrac{\pi}{3}\end{matrix}\right.\)
Ta có: \(f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{2}+\dfrac{\sqrt{3}}{2}\)
\(f\left(\dfrac{\pi}{3}\right)=\pi-\dfrac{\sqrt{3}}{2}\)
\(f\left(\pi\right)=3\pi+\sqrt{3}\)
Từ đó: \(f_{min}=f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f_{max}=f\left(\pi\right)=3\pi+\sqrt{3}\)

tìm GTLN thì đưa về dạng A^2 - k hoặc /A/ -k
GTNN đưa về dạng A^2 + k hoặc /A/ +k

Ta có :
|x - 1/2| > 0
Vậy GTNN của |x - 1/2| = 0 <=> x - 1/2 = 0 <=> x = 1/2



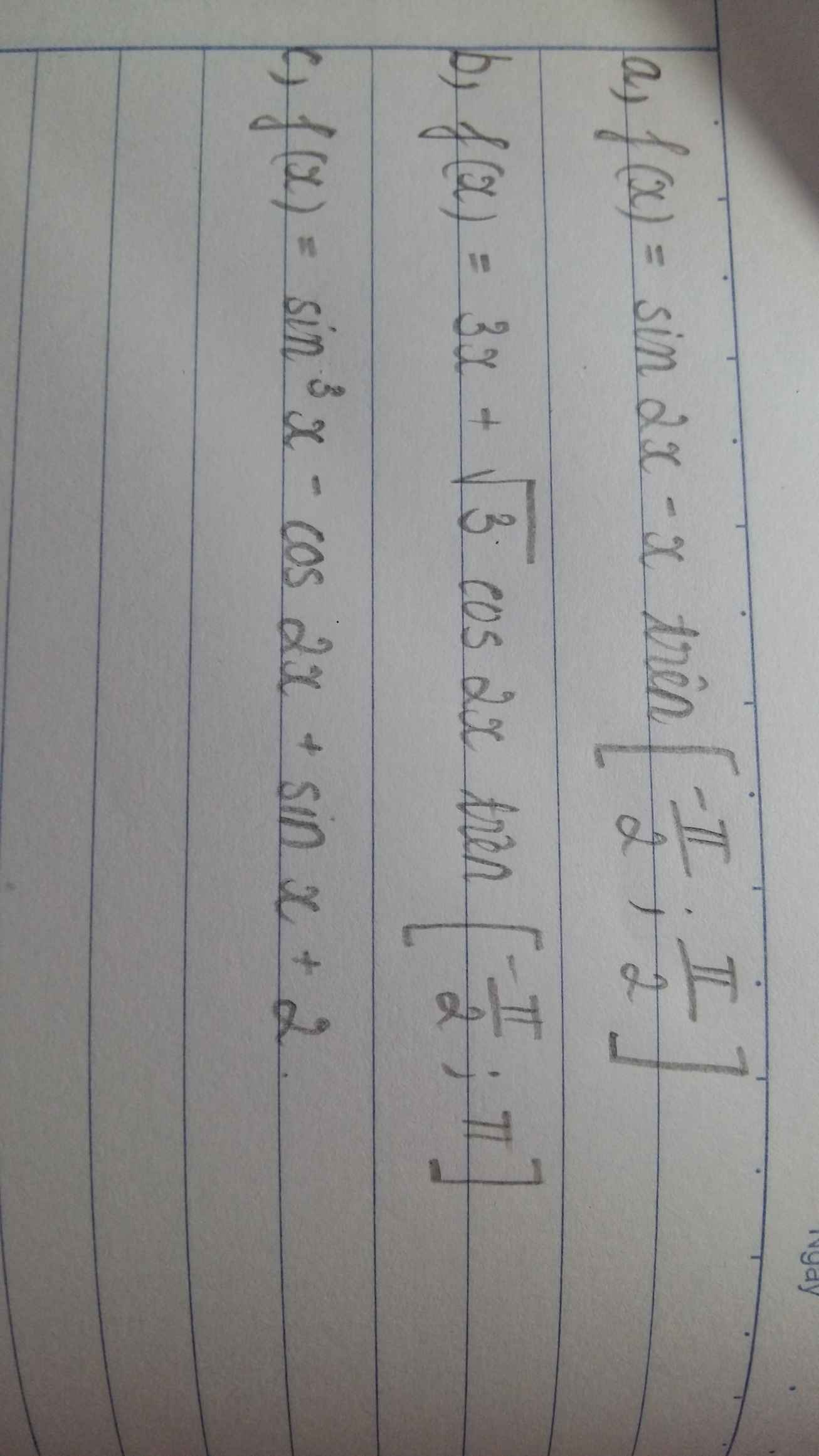
Để tìm GTNN và GTLN thì :
VD : \(\left(x+8\right)^2+2\) tìm gtnn
Ta có : \(\left(x+8\right)^2\ge0\) ( vì 2 nên phải lớn hơn không )
\(\Rightarrow\left(x+8\right)^2+2\ge2\)( +2 thì bên kia cũng cộng 2 )
Lớn hơn 2 \(\Rightarrow GTNN\) là 2 khi \(x+8=0\)
\(x=-8\)
GTLN cũng z