7/8+23/24+47/48+79/80+.......+9798/9800+10199/10200
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
5 tháng 5 2019
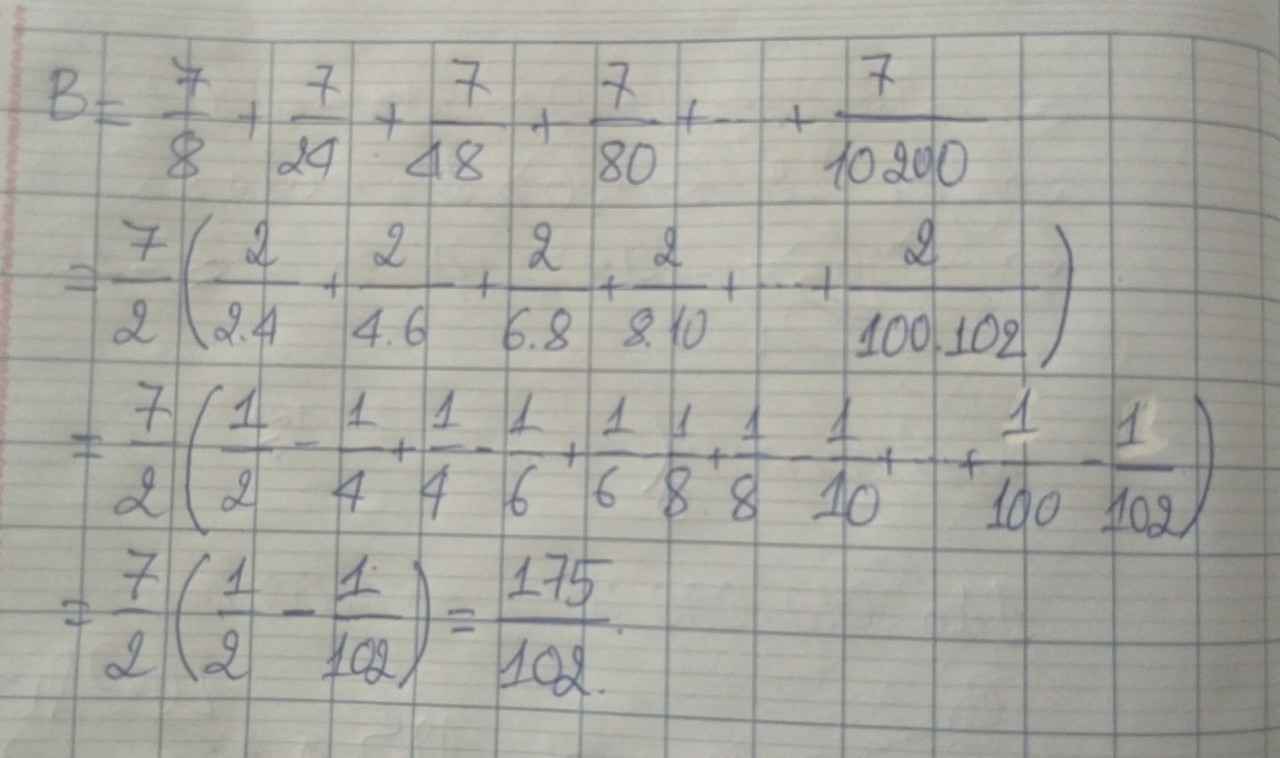
B = \(\frac{7}{2.4}+\frac{7}{4.6}+\frac{7}{6.8}+.....+\frac{7}{100.102}\)
ta có \(\frac{7}{2.4}=\frac{1}{2}\left(\frac{7}{2}-\frac{7}{4}\right);\frac{7}{4.6}=\frac{1}{2}\left(\frac{7}{4}-\frac{7}{8}\right);......;\frac{7}{100.102}=\frac{1}{2}\left(\frac{7}{100}-\frac{7}{102}\right)\)
⇒ B = \(\frac{1}{2}\left(\frac{7}{2}-\frac{7}{4}+\frac{7}{4}-\frac{7}{8}+....+\frac{7}{100}-\frac{7}{102}\right)\)
⇔ B = \(\frac{1}{2}\left(\frac{7}{2}-\frac{7}{102}\right)\)
⇔ B = \(\frac{1}{2}.\frac{175}{51}\)
⇔ B = \(\frac{175}{102}\)
MT
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
18 tháng 4 2023
A = \(\dfrac{47\times48-47\times47-24-23+2046}{2+4+8+..+512+1024}\)
Đặt tử số là B, mẫu số là C thì
B = 47\(\times\)48 - 47 \(\times\) 47 - 24 -23+2046vàC = 2 + 4 + 8 +....+ 512 + 1024
B = 47 \(\times\) 48 - 47 \(\times\) 47 - 24 - 23 + 2046
B= 47 \(\times\) 48 - 47 \(\times\) 47 - ( 24 + 23) + 2046
B = 47 \(\times\) 48 - 47 \(\times\) 47 - 47 + 2046
B = 47 \(\times\) 48 - 47 \(\times\) 47 - 47 \(\times\) 1 + 2046
B = 47 \(\times\) ( 48 - 47 - 1) + 2046
B = 47 \(\times\) 0 + 2046
B = 2046
C = 2 + 4 + 8+ ....+ 512 +1024
C \(\times\) 2 = 4 + 8 +.....+ 512 + 1024 + 2048
C \(\times\) 2 - C = 2048 - 2
C \(\times\) ( 2 - 1) = 2046
C = 2046
A = \(\dfrac{B}{C}\) = \(\dfrac{2046}{2046}\) = 1
5 tháng 8 2017
Ta có :
\(\dfrac{3}{2}\) = \(\dfrac{3}{1.2}\) = 3 x \(\dfrac{1}{1.2}\) = 3 x ( 1 - \(\dfrac{1}{2}\) ) : 2 ;
\(\dfrac{3}{8}\) = \(\dfrac{3}{2.4}\) = \(\)3 x \(\dfrac{1}{2.4}\) = 3 x ( \(\dfrac{1}{2}\) - \(\dfrac{1}{4}\) ) : 2 ;
\(\dfrac{3}{24}\) = \(\dfrac{3}{4.6}\) = 3 x \(\dfrac{1}{4.6}\) = 3. ( \(\dfrac{1}{4}\) - \(\dfrac{1}{6}\) ) : 2 ;
\(\dfrac{3}{9800}\) = \(\dfrac{3}{98.100}\) = 3 x \(\dfrac{1}{98.100}\) = 3 x ( \(\dfrac{1}{98}\) - \(\dfrac{1}{100}\) ) : 2 ;
\(\dfrac{3}{10200}\) = \(\dfrac{3}{100.102}\) = 3 x \(\dfrac{1}{100.102}\)= 3 x ( \(\dfrac{1}{100}\) - \(\dfrac{1}{102}\) )
Vậy : \(\dfrac{3}{2}\) + \(\dfrac{3}{8}\) + \(\dfrac{3}{24}\) + ........ + \(\dfrac{3}{9800}\) + \(\dfrac{3}{10200}\)
= \(\dfrac{3}{1.2}\) + \(\dfrac{3}{2.4}\) + \(\dfrac{3}{4.6}\) +........+ \(\dfrac{3}{98.100}\) + \(\dfrac{3}{100.102}\)
= 3 x ( \(\dfrac{1}{1.2}\) + \(\dfrac{1}{2.4}\) + \(\dfrac{1}{4.6}\) + .........+ \(\dfrac{1}{98.100}\) + \(\dfrac{1}{100.102}\) )
= 3 x ( \(\dfrac{2}{1.2}\) + \(\dfrac{2}{2.4}\) + \(\dfrac{2}{4.6}\) +.................+ \(\dfrac{2}{98.100}\) + \(\dfrac{2}{100.102}\) ) : 2
= 3 x ( 1 - \(\dfrac{1}{2}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{6}\) +.......+\(\dfrac{1}{98}\) - \(\dfrac{1}{100}\) + \(\dfrac{1}{100}\) - \(\dfrac{1}{102}\) ) : 2
= 3 x ( 1 - \(\dfrac{1}{102}\) ) : 2 = 3 x \(\dfrac{101}{102}\) : 2
= \(\dfrac{101}{68}\)
12 tháng 5 2021
Ta có: \(A=\dfrac{5}{8}+\dfrac{5}{24}+\dfrac{5}{48}+...+\dfrac{5}{9800}\)
\(=\dfrac{5}{2}\left(\dfrac{2}{8}+\dfrac{2}{24}+\dfrac{2}{48}+...+\dfrac{2}{9800}\right)\)
\(=\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{8}+...+\dfrac{1}{98}-\dfrac{1}{100}\right)\)
\(=\dfrac{5}{2}\left(\dfrac{1}{2}-\dfrac{1}{100}\right)\)
\(=\dfrac{5}{2}\cdot\dfrac{49}{50}\)
\(=\dfrac{245}{100}=\dfrac{49}{20}\)
16 tháng 8 2017
B = \(\frac{2}{1.3}\)+ \(\frac{2}{3.5}\)+ \(\frac{2}{5.7}\) + ..... + \(\frac{2}{99.101}\)+ \(\frac{2}{101.103}\)
= 1 - 1/3 + 1/3 - 1/5 + 1/5 - 1/7 +......+ 1/99 - 1/101 + 1/101 - 1/103
= 1- 1/103 = 102/103
10 tháng 3 2020
a)A=(-123) - 77 + (-257) +23 - 43 b)B=48+| 48-174|+(-74)
A=[(-123) - 77]+[(-257)-43]+23 B=48+(174-48)+(-74)
A= -200+(-300)+23 B=48+174+(-48)+(-74)
A= -500+23 B=[48+(-48)]+[174+(-74)]
A= -477 B=0+100=100
c)C= -2012+(-596)+(-201)+496+301 d)D=1+2-3-4+5+6-7-8+............-79-80-81
C= -2012+[(-596)+496]+[(-201)+301] D=1+(2-3-4+5)+(6-7-8+9)+............+(78-79-80-81)
C= -2010+(-100)+100 D=1+0+0+............+(-162)
C= -2010+0 D=1+(-162)
C= -2010 D= -161