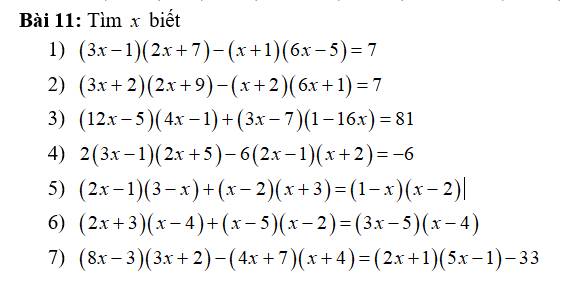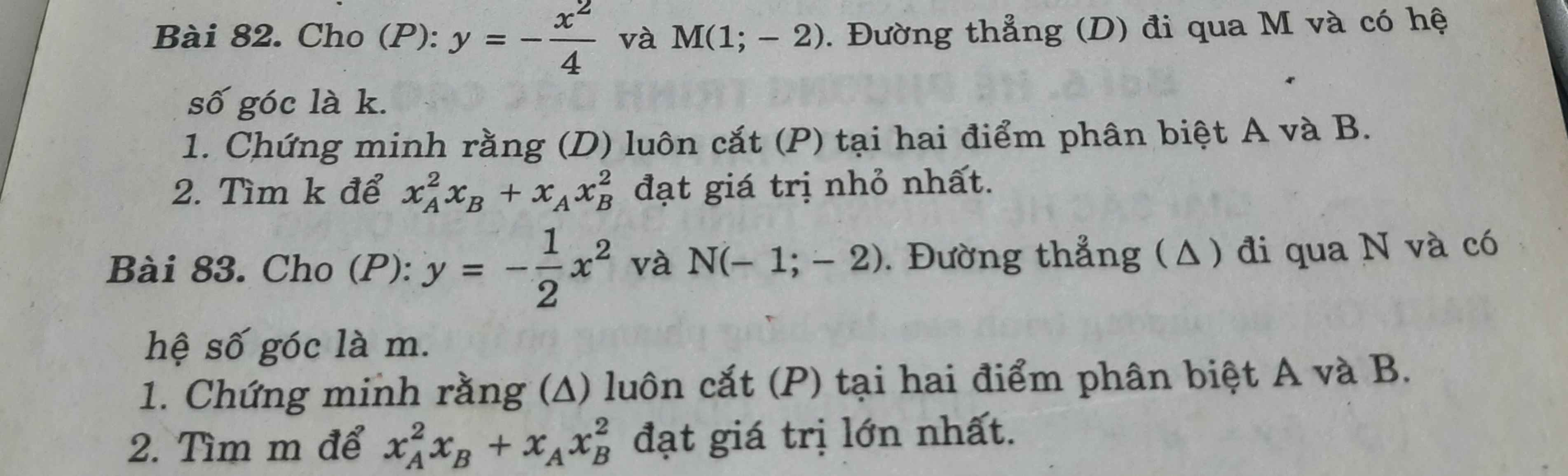Giúp nốt bài ;-;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
XM
Xuan Mai
18 tháng 4 2022
Đúng(1)
Những câu hỏi liên quan
31 tháng 8 2023
1: =>6x^2+21x-2x-7-6x^2+5x-6x+5=7
=>18x-2=7
=>18x=9
=>x=1/2
2: (3x+2)(2x+9)-(x+2)(6x+1)=7
=>6x^2+27x-4x-18-6x^2-x-12x-2=7
=>10x-20=7
=>10x=27
=>x=27/10
3: =>48x^2-12x-20x+5+3x-48x^2-7+112x=81
=>83x=83
=>x=1
4: =>2(6x^2+15x-2x-5)-6(2x^2+4x-x-2)=-6
=>12x^2+26x-10-12x^2-18x+12=-6
=>8x+2=-6
=>8x=-8
=>x=-1
5: =>6x-2x^2-3+x+x^2+x-6=-(x^2-3x+2)
=>-x^2+8x-9+x^2-3x+2=0
=>5x-7=0
=>x=7/5
6: =>2x^2-8x+3x-12+x^2-7x+10=3x^2-12x-5x+20
=>3x^2-12x-2=3x^2-17x+20
=>-12x-2=-17x+20
=>5x=22
=>x=22/5
7: =>24x^2+16x-9x-6-4x^2-16x-7x-28=10x^2-2x+5x-1-33
=>20x^2-16x-34=10x^2+3x-34
=>10x^2-19x=0
=>x(10x-19)=0
=>x=0 hoặc x=19/10
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 5 2021
Phương trình \(\Delta\) có dạng:
\(y=m\left(x+1\right)-2\Leftrightarrow y=mx+m-2\)
Phương trình hoành độ giao điểm (P) và \(\Delta\):
\(-\dfrac{1}{2}x^2=mx+m-2\Leftrightarrow x^2+2mx+2m-4=0\) (1)
\(\Delta'=m^2-2m+4=\left(m-1\right)^2+3>0\) ; \(\forall m\)
\(\Rightarrow\) (1) luôn có 2 nghiệm pb với mọi m hay (P) luôn cắt \(\Delta\) tại 2 điểm pb
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-2m\\x_Ax_B=2m-4\end{matrix}\right.\)
Đặt \(A=x_A^2x_B+x_Ax_B^2=x_Ax_B\left(x_A+x_B\right)\)
\(A=-2m\left(2m-4\right)=-4m^2+8m=-4\left(m-1\right)^2+4\le4\)
\(A_{max}=4\) khi \(m=1\)
20 tháng 10 2023
a: Xét ΔABC vuông tại A có \(cosB=\dfrac{AB}{BC}=\dfrac{1}{2}\)
nên \(\widehat{B}=60^0\)
b:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=6^2-3^2=27\)
=>\(AC=3\sqrt{3}\left(cm\right)\)
Xét ΔBAC có BD là phân giác
nên \(\dfrac{AD}{AB}=\dfrac{CD}{CB}\)
=>\(\dfrac{AD}{3}=\dfrac{CD}{6}\)
=>\(\dfrac{AD}{1}=\dfrac{CD}{2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{1}=\dfrac{CD}{2}=\dfrac{AD+CD}{1+2}=\dfrac{3\sqrt{3}}{3}=\sqrt{3}\)
=>\(\left\{{}\begin{matrix}AD=\sqrt{3}\simeq1,7\left(cm\right)\\CD=2\sqrt{3}\simeq3,5\left(cm\right)\end{matrix}\right.\)
c: ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot6=3\cdot3\sqrt{3}=9\sqrt{3}\)
=>\(AH=\dfrac{3\sqrt{3}}{2}\left(cm\right)\)
d: ΔABC vuông tại A có AH là đường cao
nên \(BA^2=BH\cdot BC\left(1\right)\)
ΔADB vuông tại A có AE là đường cao
nên \(BE\cdot BD=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BH\cdot BC=BE\cdot BD\)
=>\(\dfrac{BH}{BD}=\dfrac{BE}{BC}\)
Xét ΔBHE và ΔBDC có
BH/BD=BE/BC
\(\widehat{HBE}\) chung
Do đó: ΔBHE đồng dạng với ΔBDC
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 1
a.
Do C là giao điểm 2 tiếp tuyến tại A và M
\(\Rightarrow AC=MC\)
Tương tự có \(BD=MD\)
\(\Rightarrow AC+BD=MC+MD=CD\)
2.
Cũng theo t/c hai tiếp tuyến cắt nhau ta có:
\(\left\{{}\begin{matrix}\widehat{COA}=\widehat{COM}\\\widehat{DOB}=\widehat{DOM}\end{matrix}\right.\)
\(\Rightarrow\widehat{COA}+\widehat{COM}+\widehat{DOB}+\widehat{DOM}=2\left(\widehat{COM}+\widehat{DOM}\right)\)
\(\Rightarrow180^0=2\widehat{COD}\)
\(\Rightarrow\widehat{COD}=90^0\)
Hay tam giác COD vuông tại O
Trong tam giác vuông COD, do CD là tiếp tuyến tại M \(\Rightarrow OM\perp CD\)
\(\Rightarrow OM\) là đường cao ứng với cạnh huyền
Áp dụng hệ thức lượng:
\(OM^2=CM.MD\Rightarrow R^2=AC.BD\) (do \(AC=CM;BD=MD\))
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 1
3.1
Theo cmt ta có \(AC=MC\)
Lại có \(OA=OM=R\)
\(\Rightarrow OC\) là trung trực của AM
\(\Rightarrow OC\perp AM\) tại E
\(\Rightarrow\widehat{OEM}=90^0\)
Hoàn toàn tương tự ta có \(\widehat{OFM}=90^0\)
\(\Rightarrow OEMF\) là hình chữ nhật (tứ giác vó 3 góc vuông)
3.2
\(OM\perp CD\Rightarrow\Delta OCM\) vuông tại M
\(ME\perp OC\Rightarrow ME\) là đường cao trong tam giác vuông OCM
Áp dụng hệ thức lượng:
\(OM^2=OE.OC\Rightarrow OE.OC=R^2\)
Hoàn toàn tương tự ta có: \(OM^2=OF.OD\)
\(\Rightarrow OE.OC=OF.OD=R^2\)
3.3
Do OC là trung trực AM (chứng minh câu 3.1) \(\Rightarrow E\) là trung điểm AM
Tương tự ta có F là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác MAB
\(\Rightarrow EF||AB\)
Mà \(AB\perp BD\) (do BD là tiếp tuyến tại B)
\(\Rightarrow EF\perp BD\)
3.4
Gọi G là trung điểm CD.
Do tam giác COD vuông tại O (theo cm câu 2) \(\Rightarrow\) G là tam đường tròn ngoại tiếp tam giác COD
Hay \(GO\) là 1 bán kính của đường tròn đường kính CD (1)
\(CA\) và BD cùng vuông góc AB \(\Rightarrow CA||BD\Rightarrow ACDB\) là hình thang
O là trung điểm AB, G là trung điểm CD \(\Rightarrow OG\) là đường trung bình hình thang ACDB
\(\Rightarrow GO||DB\Rightarrow GO\perp AB\) tại G (2)
(1);(2)\(\Rightarrow AB\) là tiếp tuyến của đường tròn đường kính CD
