Ai giải giúp em âu này di ạ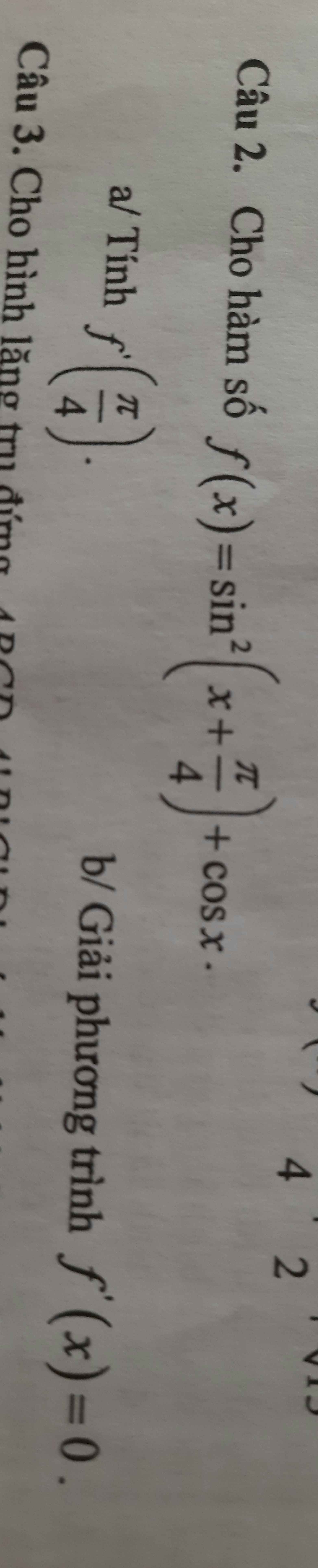
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
ai giải giúp em mấy bài toán này vs ạ giải chi tiết giúp em ạ
2
10 tháng 11 2021
\(1,\\ a,=6x^4y^4-x^3y^3+\dfrac{1}{2}x^4y^2\\ b,=4x^3+5x^2-8x^2-10x+12x+15\\ =4x^3-3x^2+2x+15\\ 2,\\ a,=7\left(x^2-6x+9\right)=7\left(x-3\right)^2\\ b,=\left(x-y\right)^2-36=\left(x-y-6\right)\left(x-y+6\right)\\ 3,\\ \Leftrightarrow x\left(x^2-0,36\right)=0\\ \Leftrightarrow x\left(x-0,6\right)\left(x+0,6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=0,6\\x=-0,6\end{matrix}\right.\)
S
21 tháng 9 2021
Xét tính trạng hình dạng cây:
\(\dfrac{Cao}{Thap}=\dfrac{9+3}{3+1}=\dfrac{3}{1}\)
=> Cao THT so với thấp
Quy ước gen: A cao. a thấp
Xét tính trạng màu sắc
\(\dfrac{Đỏ}{vang}=\dfrac{9+3}{3+1}=\dfrac{3}{1}\)
=> đỏ THT so với vàng
Quy ước gen: B đỏ. b vàng
Vì F2 thu dc tỉ lệ 9:3:3:1
=> tuân theo quy luật phân li độc lập Của Menden
=> F1 dị hợp 2 cặp giao tử. kiểu gen F1: AaBb
F1 dị hợp 2 cặp giao tử => P thuần chủng
P Cao,đỏ. x. Thấp,vàng
AABB aabb
Gp AB ab
F1: AaBb( cao,đỏ)
F1 xF1 AaBb( cao,đỏ) x AaBb( cao,đỏ)
GF1 AB,Ab,aB ab AB,Ab,aB,ab
F2: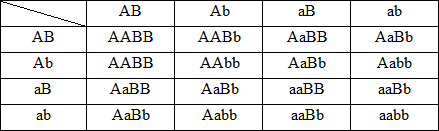
Kiểu gen: 9A_B_:3A_bb:3aaB_:1aabb
kiểu hình:9cao,đỏ :3 cao,vàng:3 thấp,đỏ:1 thấp,vàng
NT
0
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
2.
Gọi \(H\left(x;y\right)\) là toạ độ chân đường cao ứng với BC \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x-1;y+2\right)\\\overrightarrow{BC}=\left(2;1\right)\end{matrix}\right.\)
Do AH vuông góc BC \(\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow2\left(x-1\right)+y+2=0\Leftrightarrow y=-2x\)
\(\Rightarrow H\left(x;-2x\right)\Rightarrow\overrightarrow{BH}=\left(x+2;-2x-3\right)\)
Do H thuộc BC nên B, C, H thẳng hàng hay các vecto \(\overrightarrow{BC};\overrightarrow{BH}\) cùng phương
\(\Rightarrow\dfrac{x+2}{2}=\dfrac{-2x-3}{1}\Rightarrow x=\dfrac{8}{5}\Rightarrow y=-\dfrac{16}{5}\) \(\Rightarrow H\left(-\dfrac{8}{5};\dfrac{16}{5}\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(-\dfrac{13}{5};\dfrac{26}{5}\right)\Rightarrow\left\{{}\begin{matrix}AH=\sqrt{\left(-\dfrac{13}{5}\right)^2+\left(-\dfrac{6}{5}\right)^2}=\dfrac{13\sqrt{5}}{5}\\BC=\sqrt{2^2+1^2}=\sqrt{5}\end{matrix}\right.\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{13}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
3.
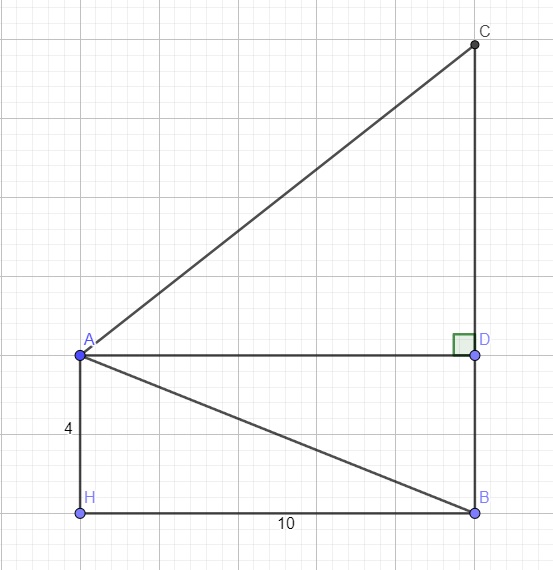
Kẻ AD vuông góc BC tại D
\(\Rightarrow AD=BH=10\) ; \(BD=AH=4\)
\(tan\widehat{BAD}=\dfrac{BD}{AD}=\dfrac{2}{5}\Rightarrow\widehat{BAD}\approx21^048'5''\)
\(\Rightarrow\widehat{CAD}=60^0-\widehat{BAD}=38^011'55''\)
\(\Rightarrow CD=AD.tan\widehat{CAD}=7,87\left(m\right)\)
\(\Rightarrow BC=BD+CD=11,87\left(m\right)\)
20 tháng 9 2021
\(1,\\ a,=3^{5+7}=3^{12}\\ b,=2^{10-3}=2^7\\ c,=2^2\cdot5^3\cdot2\cdot5=2^3\cdot5^4\\ d,=\left(3^5\cdot7^2\cdot7^2\right):\left(3^3\cdot7^3\right)=3^2\cdot7\\ 2,\\ a,=16\cdot5-2^4:2^2=80-2^2=76\\ b,=3\left(5^2+3\cdot4\right)=3\left(25+12\right)=3\cdot37=111\\ c,=49\cdot4+4\cdot6=4\left(49+6\right)=4\cdot55=220\\ d,=4^2\left(19-15\right)=4^2\cdot4=4^3=64\\ e,=249-200+36=85\\ f,=24-18:9+30=54-2=52\\ g,=36-12+48=72\\ h,=36-12+21=45\)
\(f'\left(x\right)=2sin\left(x+\dfrac{\pi}{4}\right)cos\left(x+\dfrac{\pi}{4}\right)-sinx=sin\left(2x+\dfrac{\pi}{2}\right)-sinx=cos2x-sinx\)
\(\Rightarrow f'\left(\dfrac{\pi}{4}\right)=cos\left(\dfrac{\pi}{2}\right)-sin\left(\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\)
b.
\(f'\left(x\right)=0\Leftrightarrow cos2x-sinx=0\)
\(\Leftrightarrow cos2x=sinx=cos\left(\dfrac{\pi}{2}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{2}-x+k2\pi\\2x=x-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\\x=-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)