công thức tính diện tích tam giác
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các tam giác đều có công thức tính diện tích giống nhau: \(\dfrac{1}{2}.a.h\)
Dùng công thức tính diện tích tam giác thường vào tam giác vuông được nhé bạn

Bài giải
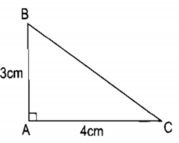
Diện tích hình tam giác đó là :
4 x 3 : 2 = 6 ( cm2 )
Đ/s : 6 cm2 .

- Diện tích hình vuông cạnh a: S = a2
- Diện tích tam giác vuông có hai cạnh góc vuông a và b là: S = 0,5 ab

\(a,S=\dfrac{1}{2}ah\) (a là cạnh đáy, h là chiều cao)
Với tam giác vuông: \(S=\dfrac{1}{2}bc=\dfrac{1}{2}ah\) (b,c là độ dài 2 cạnh góc vuông)
\(b,S_{ABC}=\dfrac{1}{2}AB\cdot AC=300\left(cm^2\right)\)

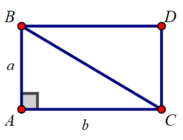
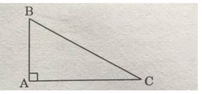
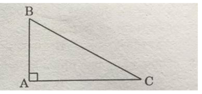
Muốn tính diện tích tam giác vuông ABC, ta dựng hình chữ nhật ABDC như trên
- ∆ABC = ∆DCB (hai cạnh góc vuông)
⇒SABC = SDCB (theo tính chất 1 diện tích đa giác) (1)
Đường chéo BC chia hình chữ nhật ABDC thành 2 phần là ∆ABC và ∆DCB
⇒SABDC = SABC + SDCB (theo tính chất 2 diện tích đa giác) (2)
Từ (1) và (2) ⇒ SABDC = 2SABC ⇒ SABC = 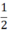 SABDC
SABDC
- ABDC là hình chữ nhật ⇒ SABDC = a.b
⇒ SABC = 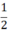 SABDC =
SABDC = 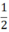 ab
ab

HÌNH CHỮ NHẬT
- Chu vi: P = (a + b) x 2 (P: chu vi)
- Diện tích: S = a x b (S: diện tích)
HÌNH VUÔNG:
- Chu vi: P = a x 4 (P: chu vi)
- Diện tích: S = a x a (S: diện tích)
HÌNH TAM GIÁC:
- Chu vi: P = a + b + c (a: cạnh thứ nhất; b: cạnh thứ hai; c: cạnh thứ ba)
- Diện tích: S = (a x h) : 2 (a: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
HÌNH BÌNH HÀNH:
- Chu vi: P = (a + b) x 2 (a: độ dài đáy)
- Diện tích: S = a x h (b: cạnh bên)
- Diện tích: S = a x h (h: chiều cao)
- Độ dài đáy: a = S : h
- Chiều cao: h = S : a
- Diện tích: S = (m x n) : 2 (m: đường chéo thứ nhất)
- Tích 2 đường chéo: (m x n) = S x 2 (n: đường chéo thứ nhất)
- HÌNH THANG
- Diện tích: S = (a + b) x h : 2 (a & b: cạnh đáy)
- Chiều cao: h = (S x 2) : a (h: chiều cao)
- Cạnh đáy: a = (S x 2) : h
HÌNH TRÒN:
- Bán kính hình tròn: r = d : 2 hoặc r = C : 2 : 3,14
- Đường kính hình tròn: d = r x 2 hoặc d = C : 3,14
- Chu vi hình tròn: C = r x 2 x 3,14 hoặc C = d x 3,14
- Diện tích hình tròn: C = r x r x 3,14
- Diện tích xung quanh: Sxq = (a x a) x 4
- Cạnh: (a x a) = Sxq : 4
- Diện tích toàn phần: Stp = (a x a) x 6
- Cạnh: (a x a) = Stp : 6
- Diện tích xung quanh: Sxq = Pđáy x h
- Chu vi đáy: Pđáy = Sxq : h
- Chiều cao: h = Pđáy x Sxq


Công thức 1: Đường phân giác trong là AD:
AD = 2/ (b + c) . căn bcp (p - a)
Công thức 2:
AD = 2bc. cosA/2 / (b + c)
Đường phân giác trong góc B và C từ đó suy ra.
Cách chứng minh công thúc 1:
Sử dụng vectơ.
theo công thức đường phân giác lớp 8 ta có DB / DC = c / b
Suy ra b.vtDB = -c.vtDC
=> b. (vtDA + vtAB) = - c. (vtDA + vtAC)
=> (b + c). vtAD = b. vtAB + c. vtAC
Bình phương hai vế có
(b+c)^2 AD^2 = 2b^2c^2 + 2bc. vtAB. vtAC
Thay vtAB.vtAC = (b^2 + c^2 - a^2) / 2 (công thức)
phân tích thành nhân tử, rút gọn có đpcm.
Cách chứng minh công thức 2:
Sử dụng diện tích:
S.ABC = S.ADB + S.ADC
bc. sinA = AD.c sinA/2 + AD.b sinA/2
2bc sinA/2 .cosA/2 = AD sinA/2 (b + c)
=> AD = 2bc.cosA/2 / (b + c)
Chú ý: Có thể dùng định lí hàm cos để tính cosA/2 thay vào công thức 2 để có công thức 1.
(vtAB là vectơ AB)
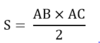
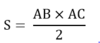
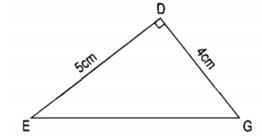
Diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài đáy, sau đó tất cả chia cho 2. Nói cách khác, diện tích tam giác thường sẽ bằng 1/2 tích của chiều cao và chiều dài cạnh đáy của tam giác.
Công thức tính diện tích hình tam giác:
S=(a x h) :2
Ta lấy:
Độ dài đáy nhân với chiều cao (cùng 1 đơn vị đo)rồi chưa cho 2