Cho tam giác ABC có 3 góc nhọn. Gọi E,M,I theo thứ tự là trung điểm của AB,AC,BC. AH là đường cao
a) chứng minh EM là trung trực của AH
b)chứng minh tứ giác EHIM là hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 7 2019
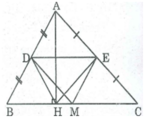
* Vì D trung điểm của AB (gt) và E trung điểm của AC (gt) nên DE là đường trung bình của tam giác ABC
⇒ DE // BC hay DE // HM
Suy ra tứ giác DEMH là hình thang
* Mà M trung điểm BC (gt) nên DM là đường trung bình của ∆ BAC
⇒ DM = 1/2 AC (tính chất đường trung bình của tam giác) (1)
* Trong tam giác vuông AHC có ∠ (AHC) = 90 0 . HE là đường trung tuyến ứng với cạnh huyền AC.
⇒ HE = 1/2 AC (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: DM = HE
Vậy hình thang DEMH là hình thang cân (vì có 2 đường chéo DM và EH bằng nhau).
6 tháng 2 2022
a: Xét ΔABC có
M là trung điểm của BA
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
=>MN=BE và MN//BE
=>BMNE là hình bình hành
b: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến
nên HM=AM
=>M nằm trên đường trung trực của AH(1)
Ta có: ΔAHC vuông tại H
mà HN là đường trung tuyến
nên HN=AC/2=AN
=>N nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra MN là đường trung trực của AH
Xét ΔABC có
M là trung điểm của AB
E là trung điểm của BC
Do đó: ME là đường trung bình
=>ME=AC/2
mà HN=AC/2
nên ME=HN
Xét tứ giác MNEH có MN//EH
nên MNEH là hình thang
mà ME=NH
nên MNEH là hình thang cân
21 tháng 12 2021
a: Xét tứ giác AEMN có
\(\widehat{AEM}=\widehat{ANM}=\widehat{NAE}=90^0\)
Do đó: AEMN là hình chữ nhật