Mn giải giúp mik vs 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(n_{CuSO_4}=0,2x\left(mol\right)\)
\(Fe+CuSO_4\rightarrow FeSO_4+Cu\)
0,2x 0,2x 0,2x
\(m_{tăng}=m_{Cu}-m_{Fe}=64\cdot0,2x-56\cdot0,2x=1,6\)
\(\Rightarrow x=1M\)
Chọn C.
\(n_{Fe}=n_{FeSO_4}=n_{Cu}=n_{CuSO_4}=0,2.x\left(mol\right)\\ Fe+CuSO_4\rightarrow FeSO_4+Cu\\ m_{t\text{ăn}g}=m_{Cu.b\text{á}m.v\text{ào}}-m_{Fe.tan.ra}\\ \Leftrightarrow1,6=64.0,2x-56.0,2x\\ \Leftrightarrow x=1\\ \Rightarrow C\)

ĐK: \(-1\le x\le1\)
Đặt \(\sqrt{1-x}=a;\sqrt{x+1}=b\Rightarrow3-x=2a^2+b^2\)
\(pt\Leftrightarrow2a-b+3ab=2a^2+b^2\)
\(\Leftrightarrow2a^2+b^2-2a+b-3ab=0\)
\(\Leftrightarrow2a^2-a\left(3b+2\right)+b^2+b=0\)
\(\Delta=\left(3b+2\right)^2-4.2.\left(b^2+b\right)=9b^2+12b+4-8b^2-8b\)
\(=b^2+4b+4=\left(b+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}a=\dfrac{3b+2-\left(b+2\right)}{4}=\dfrac{2b}{4}=\dfrac{b}{2}\Leftrightarrow2a=b\left(1\right)\\a=\dfrac{3b+2+b+2}{4}=\dfrac{4b+4}{4}=b+1\left(2\right)\end{matrix}\right.\)
pt (1) \(\Leftrightarrow2\sqrt{1-x}=\sqrt{x+1}\)
\(\Leftrightarrow4\left(1-x\right)=x+1\)
\(\Leftrightarrow5x=3\Leftrightarrow x=\dfrac{5}{3}\left(tm\right)\)
\(pt\left(2\right)\Leftrightarrow\sqrt{1-x}=1+\sqrt{x+1}\)
\(\Leftrightarrow1-x=1+x+1+2\sqrt{x+1}\)
\(\Leftrightarrow-1-2x=2\sqrt{x+1}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2+4x+1=4x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\4x^2=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\le-\dfrac{1}{2}\\\left[{}\begin{matrix}x=\dfrac{\sqrt{3}}{2}\left(l\right)\\x=-\dfrac{\sqrt{3}}{2}\left(tm\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy, pt có tập nghiệm là: \(S=\left\{-\dfrac{\sqrt{3}}{2};\dfrac{5}{3}\right\}\)

`a,` ĐKXĐ: `x>=0;x\ne1`
`A=...=(sqrtx(1+sqrtx)+sqrtx(1-sqrtx)+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(sqrtx+x+sqrtx-x+sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=(3sqrtx-3)/((1-sqrtx)(1+sqrtx))`
`=-3/(1+sqrtx)`
`b,A=-3/(1+sqrtx)`
Vì `x>=0` nên `1+sqrtx>=1` nên `3/(1+sqrtx)<=3` suy ra `A>=-3`
Dấu "=" xảy ra `<=>x=0`
Vậy `A_(min)=-3<=>x=0`

13 I wish I could help her with her business
14 The children said that they were waiting for the school bus
15 The teacher asked his students to listen to her and not to make a noise
16 My sister studied hard so she completed her exam successfully
17 She didn't decide what to wear to the party
18 She was tired so she went home yesterday
19 He has studied English for four years





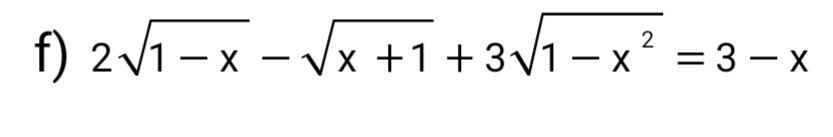 Giải pt . Mn giúp mik vs
Giải pt . Mn giúp mik vs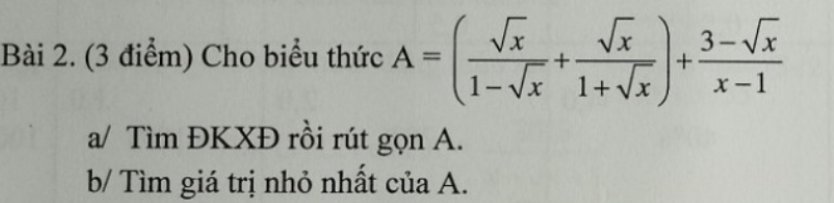
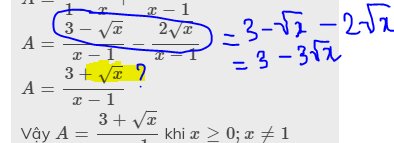

Câu 1 :
\(a,5\left(x+2\right)=2\left(x-4\right)\)
\(\Leftrightarrow5x+10=2x-8\)
\(\Leftrightarrow5x-2x=-8-10\)
\(\Leftrightarrow3x=-18\)
\(\Leftrightarrow x=-6\)
\(b,x\left(x+2\right)+3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
Vậy \(S=\left\{3;2\right\}\)
\(c,\dfrac{2x-5}{4}-\dfrac{x+1}{3}=\dfrac{1}{2}\)
\(\Leftrightarrow3\left(2x-5\right)-4\left(x+1\right)=6\)
\(\Leftrightarrow6x-15-4x-4=6\)
\(\Leftrightarrow6x-4x=6+4+15\)
\(\Leftrightarrow2x=25\)
\(\Leftrightarrow x=\dfrac{25}{2}\)
Vậy \(S=\left\{\dfrac{25}{2}\right\}\)
\(d,\dfrac{3}{x-2}-\dfrac{6}{x+2}=\dfrac{-x}{x^2-4}\left(đkxđ:x\ne\pm2\right)\)
\(\Leftrightarrow3\left(x+2\right)-6\left(x-2\right)=-x\)
\(\Leftrightarrow3x+6-6x+12=-x\)
\(\Leftrightarrow3x-6x+x=-12-6\)
\(\Leftrightarrow-2x=-18\)
\(\Leftrightarrow x=9\left(nhận\right)\)
Vậy \(S=\left\{9\right\}\)
Câu 3 :
a, Xét ΔABD và ΔHBA có :
\(\widehat{A}=\widehat{H}=90^0\)
\(\widehat{B}:chung\)
\(\Rightarrow\Delta ABD\sim\Delta HBA\left(g-g\right)\)
b, Xét ΔADH và ΔDBC có :
\(\widehat{H}=\widehat{C}=90^0\)
\(\widehat{ADH}=\widehat{DBC}\left(AB//CD,slt\right)\)
\(\Rightarrow\Delta ADH\sim\Delta DBC\)
c, Ta có : \(\Delta ABD\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BD}{AB}\)
\(\Rightarrow AB^2=BH.BD\)
d, Xét ΔABD vuông ở A , theo định lý Pi-ta-go ta được :
\(\Rightarrow BD=\sqrt{AB^2+AD^2}=\sqrt{12^2+9^2}=15\left(cm\right)\)
Ta có : \(\Delta ABD\sim\Delta HBA\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BD}{AB}\)
hay \(\dfrac{12}{BH}=\dfrac{15}{12}\)
\(\Rightarrow BH=\dfrac{12.12}{15}=9,6\left(cm\right)\)