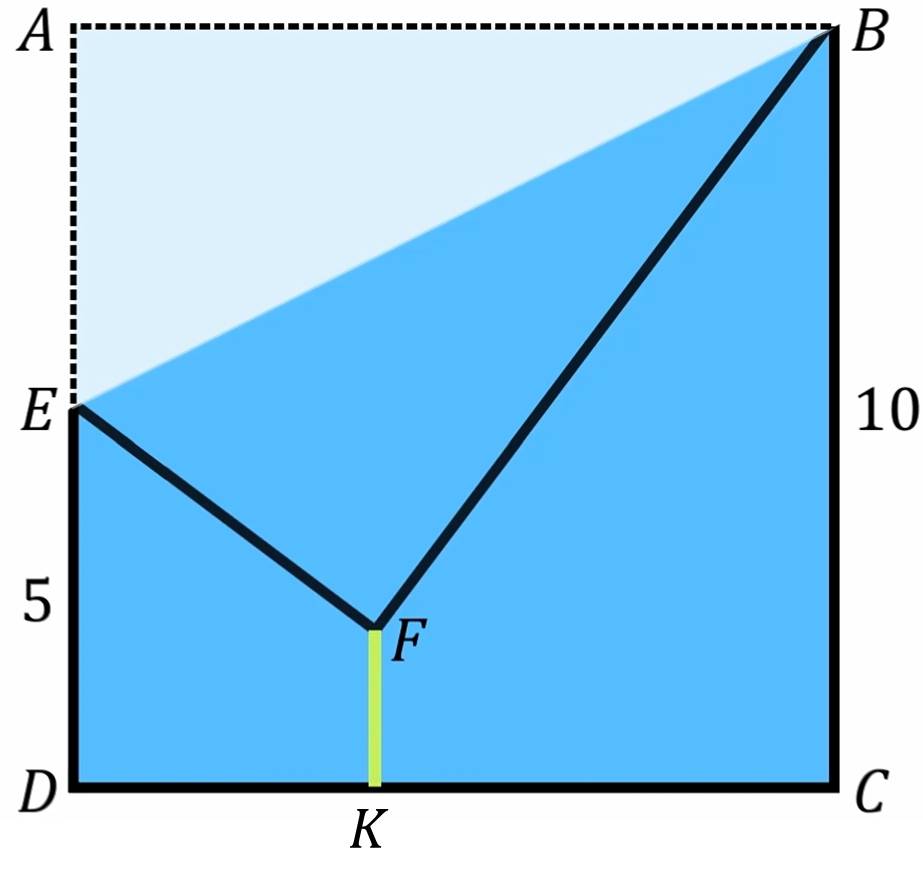
Một tờ giấy hình vuông cạnh 10 cm được gấp theo đoạn BE như hình vẽ (E là trung điểm của AD). Tính khoảng cách từ F đến CD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước 1. Gấp đôi tờ giấy.
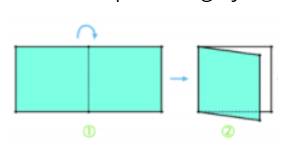
Bước 2: Vẽ một đoạn thẳng nối hai điểm tuỳ ý trên hai cạnh đối diện (cạnh không chứa nếp gấp).

Bước 3: Cắt theo đường vừa vẽ.
Bước 4. Mở tờ giấy ra ta được một hình thang cân.

Bài 2:
b: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

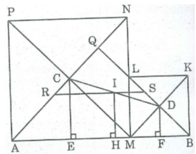
Kẻ CE ⊥ AB, IH ⊥ AB, DF ⊥ AB
Suy ra: CE // DF // IH
IC = ID (gt)
Nên IH là đường trung bình của hình thang DCEF ⇒ IH = (DF + CE) / 2
Vì C là tâm hình vuông AMNP nên ∆ CAM vuông cân tại C
CE ⊥ AM ⇒ CE là đường trung tuyến (tính chất tam giác cân)
⇒ CE = 1/2 AM
Vì D là tâm hình vuông BMLK nên ∆ DBM vuông cân tại D
DF ⊥ BM ⇒ DF là đường trung tuyến (tính chất tam giác cân)
⇒ DF = 1/2 BM
Vậy CE + DF = 1/2 AM + 1/2 BM = 1/2 (AM + BM)= 1/2 AB = a/2
Suy ra: IH = (a/2) / 2 = a/4

Đường kính hình tròn chính là cạnh của hình vuông.
Đường kính hình tròn là :
\(2\times2=4\left(cm\right)\)
Vậy cạnh của hình vuông dài \(4cm.\)
Đường kính của hình tròn:
\(2\times2=4\left(cm\right)\)
Cạnh của hình vuông bằng với đường kính hình tròn vậy cạnh của hình vuông dài 4 cm
cái này là trong bài dự thi mà. Không ăn gian.
BÁO CÁO!!!!!!!!!!