giúp mình câu 8 với ạ
K
Khách
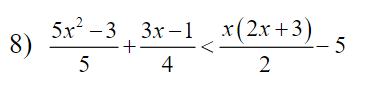
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giúp mình câu 8 với ạ
22 tháng 6 2023
8:
BC=BH+CH=64+81=145cm
\(AB=\sqrt{BH\cdot BC}=8\sqrt{145}\left(cm\right)\)
\(AC=\sqrt{81\cdot145}=9\sqrt{145}\left(cm\right)\)
tan C=AB/AC=8/9
=>góc C=42 độ
=>góc B=48 độ
24 tháng 8 2021
Bài 8:
a: Ta có: \(\sqrt{4x}=\sqrt{5}\)
\(\Leftrightarrow4x=5\)
hay \(x=\dfrac{5}{4}\)
b: Ta có: \(\sqrt{4\cdot\left(1-x\right)^2}-6=0\)
\(\Leftrightarrow2\left|x-1\right|=6\)
\(\Leftrightarrow\left|x-1\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=3\\x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
c: Ta có: \(\sqrt{2x-3}=\sqrt{7}\)
\(\Leftrightarrow2x-3=7\)
hay x=5
d: Ta có: \(\sqrt{\left(3x-2\right)^2}=4\)
\(\Leftrightarrow\left|3x-2\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=4\\3x-2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=6\\3x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{3}\end{matrix}\right.\)
NP
2
26 tháng 9 2021
\(8,\\ A=\left\{0;1;2;3\right\}\\ B=\left\{0;1;2\right\}\\ A\cap B=\left\{0;1;2\right\}\\ A\cup B=\left\{0;1;2;3\right\}\\ A\B=\left\{3\right\}\\ B\A=\varnothing\\ 9,\\ A=\left\{0;1;2;3;4\right\}\\ B=\left\{5;6\right\}\\ A\cap B=\varnothing\\ A\cup B=\left\{0;1;2;3;4;5;6\right\}\\ A\B=\left\{0;1;2;3;4\right\}\\ B\A=\left\{5;6\right\}\)
Bài cúi đúng hem :))
\(\Leftrightarrow\dfrac{4\left(5x^2-3\right)+5\left(3x-1\right)}{20}< \dfrac{10x\left(2x+3\right)-100}{20}\)
\(\Leftrightarrow4\left(5x^2-3\right)+5\left(3x-1\right)< 10x\left(2x+3\right)-100\)
\(\Leftrightarrow20x^2-12+15x-5< 20x^2+30x-100\)
\(\Leftrightarrow-15x< -83\)
\(\Leftrightarrow x>\dfrac{83}{15}\)
Vậy \(S=\left\{x|x>\dfrac{83}{15}\right\}\)
\(8,\dfrac{5x^2-3}{5}+\dfrac{3x-1}{4}< \dfrac{x\left(2x+3\right)}{2}-5\)
\(\Leftrightarrow4\left(5x^2-3\right)+5\left(3x-1\right)< 10x\left(2x+3\right)-100\)
\(\Leftrightarrow20x^2-12+15x-5< 20x^2+30x-100\)
\(\Leftrightarrow20x^2-20x^2+15x-30x-12-5+100< 0\)
\(\Leftrightarrow-15x+83< 0\)
\(\Leftrightarrow-15x< -83\)
\(\Leftrightarrow x>\dfrac{83}{15}\)
Vậy \(S=\left\{x\left|x>\dfrac{83}{15}\right|\right\}\)