cho tam giác ABC vuông tại A,AB bằng 9,AC bằng 12,BC bằng 15,cho phân giác góc C cắt AB tại N tính NB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
=>BH/BA=BA/BC
=>BA^2=BH*BC
b: BC=căn 9^2+12^2=15cm
AH=9*12/15=7,2cm

a: BC=15cm
b: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó:ΔBAD=ΔBHD
c: Xét ΔADK vuông tại A và ΔHDC vuông tại H có
DA=DH
\(\widehat{ADK}=\widehat{HDC}\)
Do đó:ΔADK=ΔHDC
Suy ra: DK=DC và AK=HC
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC

a. Vì AD là tia phân giác góc A
=> BAD = BAC
Xét tam giác BAD và tam giác BAC:
AB chung
BAD = CAD (cmt)
AB = AC( tam giác ABC cân tại A)
=> tam giác BAD = tam giác CAD (cgc)
b. Vì tam giác BAD = tam giác CAD (cmt)
=> BD = CD(hai góc tương ứng) (đpcm)
c. Vì DM ⊥ AB (M ∈ AB)
=> M = 90o
Vì DN ⊥ AC (N ∈ AC)
=> N = 90o
Xét tam giác BDM và tam giác CDN :
M = N (=90o)
BD = CD (cmb)
B = C(tam giác ABC cân tại A)
=>tam giác BDM = tam giác CDN(ch-gn)(đpcm)
=> DM = DN (2 cạnh tương ứng)
d. Xét tam giác AMD và tam giác AND:
DM = DN(cmc)
M = N(=90o)\
AD chung
=> tam giác AMD = tam giác AND (ch-cgv) (đpcm)

a: BC=căn 13^2-5^2=12cm
Xét ΔACE vuông tại C và ΔAKE vuông tại K có
AE chung
góc CAE=góc KAE
=>ΔACE=ΔAKE
b: CE=KE
KE<EB
=>CE<EB
c: góc BCK+góc ACK=90 độ
góc HCK+góc AKC=90 độ
mà góc ACK=góc AKC
nên góc BCK=góc HCK
=>CK là phân giác của góc HCB

Tự vẽ hình
a,AD ĐL py-ta-go vào \(\Delta\)vuông ABC có
\(BC^2=AB^2+AC^2\)
\(x^2=9^2+12^2\)
\(x^2=81+144\)
\(x^2=225\)
\(x=\sqrt{225}=15\)
b,Xét \(\Delta BAN\)và \(\Delta CDN\)có:
BN=DN
\(\widehat{BNA}=\widehat{DNC}\)
NA=NC
\(\Rightarrow\Delta BNA=\Delta CDN\left(c.g.c\right)\)
c,Vì \(\Delta BNA=\Delta CND\left(cmt\right)\)
\(\Rightarrow\widehat{BAN}=\widehat{DCN}\)(2 cạnh t.ư)
Mà 2 góc này ở VTSLT
\(\Rightarrow CD//AB\)

a) Xét tam giác ABD và tam giác EBD có
BAD=BED(=90 ĐỘ)
ABD=EBD ( BD là tia pg của ABC)
BD cạnh chug
Do đó t/giác ABD= t/ giác EBD(chgn)
b) Vì t/giác ABC vuông ở A nên
suy ra AB^2+AC^2=BC^2 ( đl PY TA GO)
AB^2+12^2=15^2
AB^2+144=225
AB^2=81
AB^2=9^2
AB=9 cm
Mà AB=BE( t/giác ABD=t/giác EBD)
Do đó BE=9 cm
( sr bạn nhé í c mình chx nghĩ ra![]() ☹)
☹)
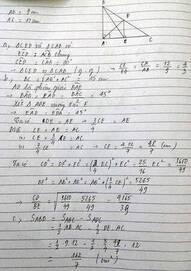
Xét ΔBAC có CN là phân giác
nên NA/AC=NB/BC
=>NA/12=NB/15
=>NA/4=NB/5
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{NA}{4}=\dfrac{NB}{5}=\dfrac{NA+NB}{4+5}=\dfrac{9}{9}=1\)
Do đó: NB=5cm