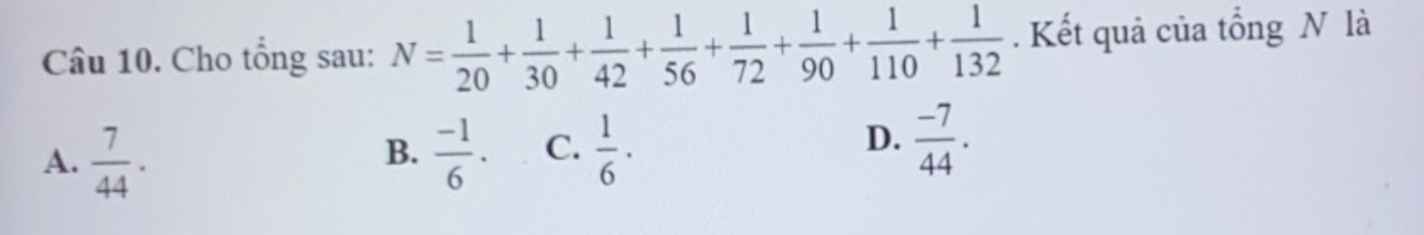
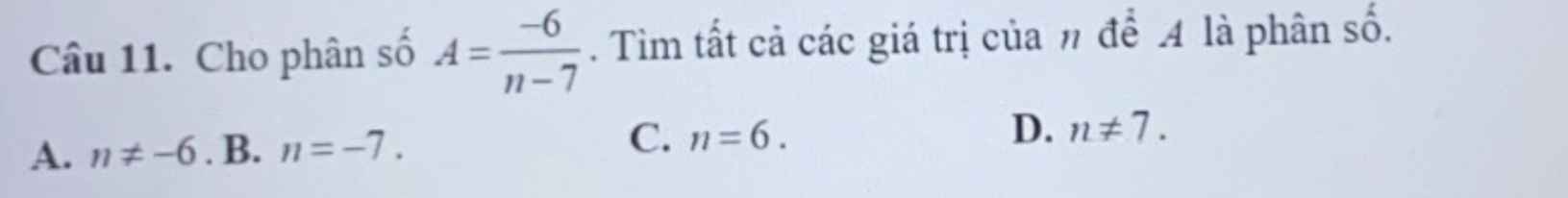
mng giúp mk vs ạ :3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QN
0
AH
Akai Haruma
Giáo viên
22 tháng 2 2021
Lời giải:
\(\lim\limits_{x\to 2}\frac{x^2+ax+b}{2x^2-x-6}=\lim\limits_{x\to 2}\frac{x^2+ax+b}{(x-2)(2x+3)}\)
Để giới hạn này là hữu hạn thì $x^2+ax+b\vdots x-2$
$\Rightarrow 2^2+a.2+b=0\Leftrightarrow 2a+b=-4$
Đáp án A.
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2021
\(2x^2-x-6=0\) có 1 nghiệm \(x=2\)
Do đó giới hạn đã cho là hữu hạn khi và chỉ khi \(x^2+ax+b=0\) cũng có 1 nghiệm \(x=2\)
\(\Rightarrow4+2a+b=0\Rightarrow b=-2a-4\)
Vậy:
\(\lim\limits_{x\rightarrow2}\dfrac{x^2+ax-2a-4}{2x^2-x-6}=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+2\right)+a\left(x-2\right)}{\left(x-2\right)\left(2x+3\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(x+a+2\right)}{\left(x-2\right)\left(2x+3\right)}=\lim\limits_{x\rightarrow2}\dfrac{x+a+2}{2x+3}=\dfrac{a+4}{7}\)
\(\Rightarrow\dfrac{a+4}{7}=\dfrac{3}{2}\Rightarrow a=\dfrac{13}{2}\Rightarrow b=-2a-4=-17\)
\(\Rightarrow2a+b=-4\)
MA
0
E
6 tháng 3 2020
Ta có : (-1)+3+(-5)+7+.....+[-(x-2)+x]=600
[(-1)+3]+[(-5)+7]+.....+[-(x-2)]+x=600
2 + 2 + .... + 2 = 600
2 . (1+1+ ...... + 1 ) = 600
\(\Leftrightarrow\) 1 + 1 + .... + 1 = 600 : 2
\(\Leftrightarrow\)1 + 1 + ..... + 1 = 300
Số dấu [] là : (x - 3 ) : 4 + 1
\(\Rightarrow\)(x - 3 ) : 4 + 1 = 300
\(\Rightarrow\)(x-3) : 4 = 299
\(\Rightarrow\)x - 3 = 299 x 4
\(\Rightarrow\)x - 3 = 1196
\(\Rightarrow\)x = 1196 + 3
\(\Rightarrow\)x = 1199
Vậy x = 1199.
# HOK TỐT #
12 tháng 1
a: Ta có: \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
\(\widehat{ACB}=\widehat{ECN}\)(hai góc đối đỉnh)
Do đó: \(\widehat{ABC}=\widehat{ECN}\)
Xét ΔMBD vuông tại D và ΔNCE vuông tại E có
BD=CE
\(\widehat{MBD}=\widehat{NCE}\)
Do đó: ΔMBD=ΔNCE
=>DM=EN
b: Ta có: DM\(\perp\)BC
EN\(\perp\)BC
Do đó: DM//EN
Xét ΔIDM vuông tại D và ΔIEN vuông tại E có
MD=EN
\(\widehat{MDI}=\widehat{ENC}\)(hai góc so le trong, DM//EN)
Do đó: ΔIDM=ΔIEN
=>IM=IN
=>I là trung điểm của MN
MA
2
23 tháng 12 2021
g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
23 tháng 12 2021
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
C
C