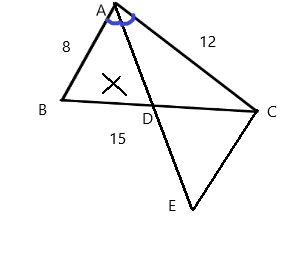
Cho tam giác ABC. Tia phân giác góc A cắt BC tại D. Qua C kẻ đường thẳng song song với AB cắt AD tại E. a) Chứng minh: ∆ABD ∽ ∆ECD b) Cho AB = 8cm, AC = 12cm, BC =15cm. Tính DB, DC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)
\(\widehat{ABD}=\widehat{ECD}\)
Do đó; ΔABD\(\sim\)ΔECD
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{2}=\dfrac{DC}{3}=\dfrac{DB+DC}{2+3}=\dfrac{15}{5}=3\)
Do đó: DB=6cm; DC=9cm

a) Vì AB//CE (gt)
=> BAD = CED (so le trong)
Xét tam giác ABD và tam giác ECD có
BAD = CED (cmt)
ADB = EDC (đối đỉnh)
=> Tam giác ABD đồng dạng với tam giác ECD
b) Đặt BD là x, ta có:
CD = BC - BD = 15 - x
Xét tam giác ABC có AD là đường phân giác (gt) nên
=> BD/DC = AB/AC (Tính chất đường phân giác trong tam giác)
Thay số: x/15 - x = 8/12
=> 12x = 8(15 - x)
(=) 12x = 120 - 8x
(=) 20x = 120
(=) x = 6
=> BD = 6
=> CD = BC - BD = 15 - 6 = 9 cm

a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)
\(\widehat{ABD}=\widehat{ECD}\)
Do đó; ΔABD\(\sim\)ΔECD
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{2}=\dfrac{DC}{3}=\dfrac{DB+DC}{2+3}=\dfrac{15}{5}=3\)
Do đó: DB=6cm; DC=9cm

a: Xét ΔABD và ΔECD có
\(\widehat{ADB}=\widehat{EDC}\)
\(\widehat{ABD}=\widehat{ECD}\)
Do đó; ΔABD\(\sim\)ΔECD
b: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{DB}{2}=\dfrac{DC}{3}=\dfrac{DB+DC}{2+3}=\dfrac{15}{5}=3\)
Do đó: DB=6cm; DC=9cm

Gọi Bx là tia đối của tia BA. Lấy E trên AC sao cho AB = AE
Xét tam giác BAD=EAD c-g-c => BD = DE và DEC = CBx
Trong tam giác ABC, BAC + ABC + ACB = 180 => ACB = 180 - BAC - ABC => ACB < 180 - ABC
Ta có DBx + ABC = 180 (hai góc kề bù) => DBx = 180 - ABC
=>ACB < DBx => ACB < DEC => Trong tam giác DEC, DC > DE (Quan hệ giữa góc và cạnh)
Vậy BD < DC

a) ta có
goc BAD+ goc DAC =90 (2 góc kề phụ)
goc ADB+goc HAD=90 ( tam giác AHD vuông tại H)
goc DAC=goc HAD (AD lả p/g goc HAC)
==> góc BAD= goc ADB
-> tam giac BAD cân tại B
b) xet tam giac ADH và tam giac ADE ta có
AD= AD ( cạnh chung)
goc HAD = goc DAC ( AD là p/g goc HAC)
goc AID = góc AIE (=90)
--> tam giac ADH= tam giac ADE (g-c-g)
-< AH= AE ( 2 canh tương ứng)
Xét tam giac AHD và tam giac AED ta có
AD=AD ( cạnh chung)
AH=AE (cmt)
goc DAH= goc DAE ( AD là p/g HAC)
-> tam giac AHD= tam giac AED ( c-g-c)
-> goc AHD= goc AED ( 2 góc tương ứng
mà góc AHD = 90 ( AH vuông góc BC)
nên AED =90
-> DE vuông góc AC
c) Xét tam giac ABH vuông tại H ta có
AB2= AH2+BH2 ( dly pi ta go)
152=122+BH2
BH2 =152-122=81
BH=9
ta có BA=BD ( tam giác ABD cân tại B)
BA=15 cm (gt)
-> BD=15
mà BH+HD=BD ( H thuộc BD)
nên 9+HD=15
HD=15-9=6
Xét tam giác ADH vuông tại H ta có
AD2=AH2+HD2 ( định lý pitago)
AD2=122+62=180
-> AD=\(\sqrt{180}=6\sqrt{5}\)
a) Vì BD = BA nên ΔΔBAD cân tại B
=> BADˆBAD^góc BAD = g BDA (góc đáy) →→-> đpcm
b) Ta có: góc BAD + g DAC = 90o
=> g DAC = 90o - g BAD (1)
Áp dụng tc tam giác vuông ta có:
g HAD + g BDA = 90o
=> g HAD = 90o - g BDA (2)
mà góc BAD = g BDA (câu a)
=> gDAC = g HAD
=> AD là tia pg của g HAC.
c) Áp dụng tc tổng 3 góc trong 1 tg ta có:
g AHD + g HDA + g HAD = 180o
=> 90o + g HDA + g HAD = 180o
=> g HDA + g HAD = 90o (3)
g DAC + g DKA + g ADK = 180o
=> g DAC + 90o + g ADK = 180o
=> g DAC + g ADK = 90o (4)
mà gDAC = g HAD hay gDAK = gHAD
Xét tgHAD và tgKAD có:
g HDA = g ADK (c/m trên)
AD chung
g HAD = g DAK (c/m trên)
=> tgHAD = tgKAD (g.c.g)
=> AH = AK (2 cạnh t/ư)

a: Xét ΔABD và ΔECD có
góc ADB=góc EDC
góc ABD=góc ECD
=>ΔABD đồng dạng với ΔECD
b: AD là phân giác
=>DB/AB=DC/AC
=>DB/8=DC/12
=>DB/2=DC/3=(DB+DC)/(2+3)=15/5=3
=>DB=6cm; DC=9cm