Cho số phức z thỏa mãn \(z^4=476+480i\). Tìm z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
11 tháng 8 2018
Chọn A.
Ta có ![]()
Giải bất phương trình trên với ẩn |z| ta được:
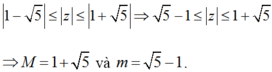
Vậy ![]()

CM
5 tháng 8 2018
Đáp án A
Phương pháp
Gọi ![]()
Sử dụng định nghĩa hai số phức bằng nhau.
Cách giải
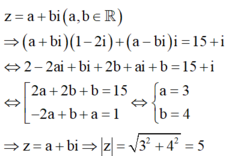

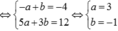
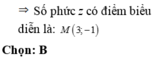



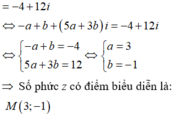
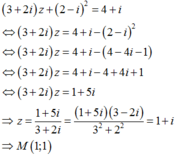


Lời giải:
Đặt $z=a+bi$ với $a,b\in\mathbb{R}$.
$z^4=476+480i$
$\Leftrightarrow (a+bi)^4=476+480i$
$\Leftrightarrow (a^2-b^2+2abi)^2=476+480i$
$\Leftrightarrow (a^2-b^2)^2-4a^2b^2+4ab(a^2-b^2)i=476+480i$
\(\Rightarrow \left\{\begin{matrix} (a^2-b^2)^2-4a^2b^2=476\\ ab(a^2-b^2)=120\end{matrix}\right.(*)\)
Đặt $ab=x; a^2-b^2=y$ thì: \(\left\{\begin{matrix} y^2-4x^2=476\\ xy=120\end{matrix}\right. \Rightarrow \left\{\begin{matrix} y^2=4x^2+476\\ x^2y^2=14400\end{matrix}\right.\)
\(\Rightarrow x^2(4x^2+476)=14400\)
$\Rightarrow x^2=25$
$\Rightarrow x=\pm 5\Rightarrow y=\pm 24$
Nếu $x=5$ và $y=24$ thì $ab=5; a^2-b^2=24$
$\Leftrightarrow a^2(-b^2)=-25; a^2+(-b^2)=24$. Theo Viet đảo thì $a^2,-b^2$ là nghiệm của PT $X^2-24X-25=0$
$\Rightarrow a^2=25; b^2=1$. Kết hợp với $(*)$ suy ra $(a,b)=(5,1),(-5,-1)$
$\Rightarrow z=5+i$ hoặc $-5-i$
Trường hợp còn lại tương tự thì $z=\pm (1-5i)$