làm chi tiết một chút júp mình ạ
K
Khách
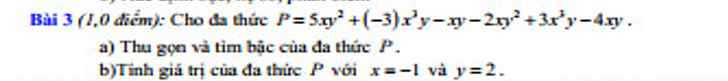
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 5 2021
Ta có
\(a^2+1=a^2+ab+bc+ca=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right).\left(a+c\right)\\ Cmtt:b^2+1=\left(b+a\right).\left(b+c\right)\\ c^2+1=\left(c+a\right).\left(c+b\right)\)
Nên
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\\ =\dfrac{\left(b-c\right)}{\left(a+b\right)\left(a+c\right)}+\dfrac{\left(c-a\right)}{\left(b+c\right)\left(b+a\right)}+\dfrac{\left(a-b\right)}{\left(c+a\right)\left(c+b\right)}\\ =\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(c+a\right)+\left(a-b\right)\left(a+b\right)}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\\ =0\)
26 tháng 5 2021
\(\dfrac{b-c}{a^2+1}+\dfrac{c-a}{b^2+1}+\dfrac{a-b}{c^2+1}\)
\(=\dfrac{b-c}{a^2+ab+bc+ac}+\dfrac{c-a}{b^2+ab+bc+ca}+\dfrac{a-b}{c^2+ab+bc+ca}\)
\(=\dfrac{b-c}{a\left(a+b\right)+c\left(a+b\right)}+\dfrac{c-a}{b\left(a+b\right)+c\left(a+b\right)}+\dfrac{a-b}{c\left(c+a\right)+b\left(a+c\right)}\)
\(=\dfrac{b-c}{\left(a+c\right)\left(a+b\right)}+\dfrac{c-a}{\left(b+c\right)\left(a+b\right)}+\dfrac{a-b}{\left(b+c\right)\left(a+c\right)}\)
\(=\dfrac{\left(b-c\right)\left(b+c\right)+\left(c-a\right)\left(a+c\right)+\left(a-b\right)\left(a+b\right)}{\left(a+c\right)\left(a+b\right)\left(b+c\right)}\)
\(=\dfrac{b^2-c^2+c^2-a^2+a^2-b^2}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=0\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2021
\(sin^2x=\left(sinx\right)^2\ne sin\left(x^2\right)\)
1 cái là bình phương của cả hàm sin, 1 cái chỉ là bình phương của góc
Cách giải bài này: suy nghĩ đầu tiên: hạ bậc.
Đầu tiên chắc chắn là phải biến đổi \(-sin^2a-sin^2b\) (phần \(sin^2\left(a+b\right)\) nếu áp dụng \(sin^2\left(a+b\right)=\left(sina.cosb+cosa.sinb\right)^2\) thì khai triển ra sẽ rất thảm họa nên cứ để đó từ từ tính sau)
\(-sin^2a-sin^2b=-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2a\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2b\right)\) (công thức hạ bậc)
\(=-1+\dfrac{1}{2}\left(cos2a+cos2b\right)=-1+cos\left(a+b\right)cos\left(a-b\right)\) (công thức biến tổng thành tích)
Thấy xuất hiện góc \(\left(a+b\right)\) giống góc của \(sin^2\left(a+b\right)\) rồi, nhưng của hàm cos, vậy thì đơn giản hãy biến \(sin^2\left(a+b\right)\) thành hàm cos bằng công thức cơ bản: \(sin^2\left(a+b\right)=1-cos^2\left(a+b\right)\)
Do đó, chắc chắn bài toán sẽ được giải quyết như sau:
\(A=1-cos^2\left(a+b\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2a\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2b\right)\)
\(A=-cos^2\left(a+b\right)+\dfrac{1}{2}\left(cos2a+cos2b\right)\)
\(A=-cos^2\left(a+b\right)+cos\left(a+b\right)cos\left(a-b\right)\)
\(=cos\left(a+b\right)\left[cos\left(a-b\right)-cos\left(a+b\right)\right]\)
\(=2sina.sinb.cos\left(a+b\right)\)
(Sử dụng biến tổng thành tích: \(cosx-cosy=-2sin\dfrac{x+y}{2}sin\dfrac{x-y}{2}\)
Thì: \(cos\left(a-b\right)-cos\left(a+b\right)=-2sin\dfrac{a-b+a+b}{2}sin\dfrac{a-b-a-b}{2}=-2sina.sin\left(-b\right)=2sina.sinb\)
CT
2
2 tháng 1 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{2x-y}{2\cdot3-5}=11\)
Do đó: x=33; y=55
NT
1
13 tháng 12 2021
TL
2161 = (24)161 / 4 = 16161 / 4
So sánh : 13 < 16 ; 40 < 161 / 4 ( = 40, 25 )
=> 1340 < 2161
Khi nào rảnh vào kênh H-EDITOR xem vid nha!!! Thanks!
27 tháng 5 2022
\(\left(x+2\right)\left(\dfrac{360}{x}-6\right)=360\)
\(ĐK:x\ne0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{360-6x}{x}\right)=360\)
\(\Leftrightarrow360-6x+\dfrac{720-12x}{x}=360\)
\(\Leftrightarrow360x-6x^2+720-12x=360x\)
\(\Leftrightarrow6x^2+12x-720=0\)
\(\Delta=12^2-4.6.\left(-720\right)\)
\(=17424>0\)
`->` pt có 2 nghiệm
\(\left\{{}\begin{matrix}x_1=\dfrac{-12-\sqrt{17424}}{12}=-12\\x_2=\dfrac{-12+\sqrt{17424}}{12}=10\end{matrix}\right.\) ( tm )
Vậy \(S=\left\{-12;10\right\}\)
10 tháng 1
Bài 10:
a: \(A=\dfrac{10}{11}+\dfrac{1}{11}\cdot\dfrac{3}{11}+\dfrac{1}{11}\cdot\dfrac{8}{11}\)
\(=\dfrac{10}{11}+\dfrac{1}{11}\left(\dfrac{3}{11}+\dfrac{8}{11}\right)\)
\(=\dfrac{10}{11}+\dfrac{1}{11}=\dfrac{11}{11}=1\)
b: \(B=\dfrac{5}{7}\cdot\dfrac{40}{11}-\dfrac{5}{11}\cdot\dfrac{117}{7}\)
\(=\dfrac{5}{7}\left(\dfrac{40}{11}-\dfrac{117}{11}\right)\)
\(=\dfrac{5}{7}\cdot\dfrac{-77}{11}=\dfrac{5}{7}\cdot\left(-7\right)=-5\)
c: \(C=\dfrac{3}{7}\cdot\dfrac{9}{11}+\dfrac{3}{7}\cdot\dfrac{5}{11}-\dfrac{3}{7}\cdot\dfrac{25}{11}\)
\(=\dfrac{3}{7}\left(\dfrac{9}{11}+\dfrac{5}{11}-\dfrac{25}{11}\right)\)
\(=\dfrac{3}{7}\cdot\dfrac{-11}{11}=-\dfrac{3}{7}\)
d: \(D=\dfrac{5}{7}\cdot\dfrac{-3}{38}\cdot\dfrac{7}{10}\cdot\dfrac{19}{6}\)
\(=\dfrac{5}{7}\cdot\dfrac{7}{10}\cdot\dfrac{-3}{6}\cdot\dfrac{19}{38}\)
\(=\dfrac{5}{10}\cdot\dfrac{-1}{2}\cdot\dfrac{1}{2}=\dfrac{-1}{8}\)
Bài 11:
a: Sau hai ngày thì lượng sữa còn lại chiếm:
\(1-\dfrac{1}{5}-\dfrac{1}{4}=1-\dfrac{9}{20}=\dfrac{11}{20}\)(hộp)
b: Lượng sữa còn lại sau 2 ngày là:
\(1000\cdot\dfrac{11}{20}=550\left(ml\right)\)
2
27 tháng 5 2022
`48/[x+4]+48/[x-4]=5` `ĐK: x \ne +-4`
`<=>[48(x-4)+48(x+4)]/[(x-4)(x+4)]=[5(x+4)(x-4)]/[(x-4)(x+4)]`
`=>48x-192+48x+192=5x^2-80`
`<=>5x^2-96x-80=0`
`<=>5x^2-100+4x-80=0`
`<=>5x(x-20)+4(x-20)=0`
`<=>(x-20)(5x+4)=0`
`<=>` $\left[\begin{matrix} x=20\\ x=\dfrac{-4}{5}\end{matrix}\right.$ (t/m)
Vậy `S={-4/5;20}`
TC
27 tháng 5 2022
ĐK : \(x\ne\pm4\)
\(\Leftrightarrow\cdot\dfrac{48\left(x+4\right)+48\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5\left(x+4\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow48x+192+48x-192==5x^2-80\)
\(\Leftrightarrow96x=5x^2-80\)
\(\Leftrightarrow5x^2-96x-80=0\)
\(\Leftrightarrow5x^2+4x-100-80=0\)
\(\Leftrightarrow4\left(x-20\right)+5x\left(x-20\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-20=0\\5x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=20\\x=-\dfrac{4}{5}\end{matrix}\right.\)
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
NM
7 tháng 3 2021
Hoàn cảnh:
- Trong nửa sau thế kỉ XIX, nền kinh tế Việt Nam tiếp tục lâm vào tình trạng khủng hoảng nghiêm trọng.
- Để đối phó với tình hình đó, triều đình nhà Nguyễn đã tăng cường bóc lột nhân dân, thậm chí áp dụng cả những biện pháp tiêu cực như: cho nộp tiền chuộc tội, cho buôn bán thuốc phiện, mua quan bán tước…
- Nhiều cuộc khởi nghĩa và bạo loạn chống triều đình đã nổ ra. Mặc dù, các cuộc khởi nghĩa đều bị dập tắt, nhưng đã làm cho tài lực và binh lực nhà Nguyễn thêm suy sụp. Mẫu thuấn giữa các tầng lớp nhân dân với giai cấp phong kiến thống trị ngày càng trở lên sâu sắc. Trong khi đó thực dân Pháp đang ráo riết chuẩn bị xâm lược nước ta,
- Vận nước nguy nan đã tác động tới quan lại, sĩ phu yêu nước tiến bộ.Nhiều đề nghị cải cách Duy Tân đã được đề ra.
Nội dung cơ bản:
- Nguyễn Trường Tộ: gửi lên triều đình 30 bản điều trần, yêu cầu chấn chỉnh bộ máy quan lại, phát triển công, thương nghiệp, tài chính, chỉnh đốn võ bị, mở rộng ngoại giao, cải tổ giáo dục
- Nguyễn Lộ Trạch: dân hai bản "Thời vụ sách", đề nghị chấn hưng dân khí, khai thông dân trí, bảo vệ đất nước.
\(a,P=5xy^2+\left(-3\right)x^2y-xy-2xy^2+3x^2y-4xy=3xy^2-5xy\)
Bậc: 3
b, Thay x=-1, y=2 vào pt ta có:
\(P=3xy^2-5xy=3.\left(-1\right).2^2-5.\left(-1\right).2=-3.4+5.2=-12+10=-2\)