Giải phương trình \(4\left(x-\sqrt{5-x}\right)\left(\sqrt{5-x}+3\right)=\left(x+3\right)^2\)
Cần gấp !!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyễn Thành Long
20 tháng 3 2022
Đúng(1)
Những câu hỏi liên quan
26 tháng 5 2021
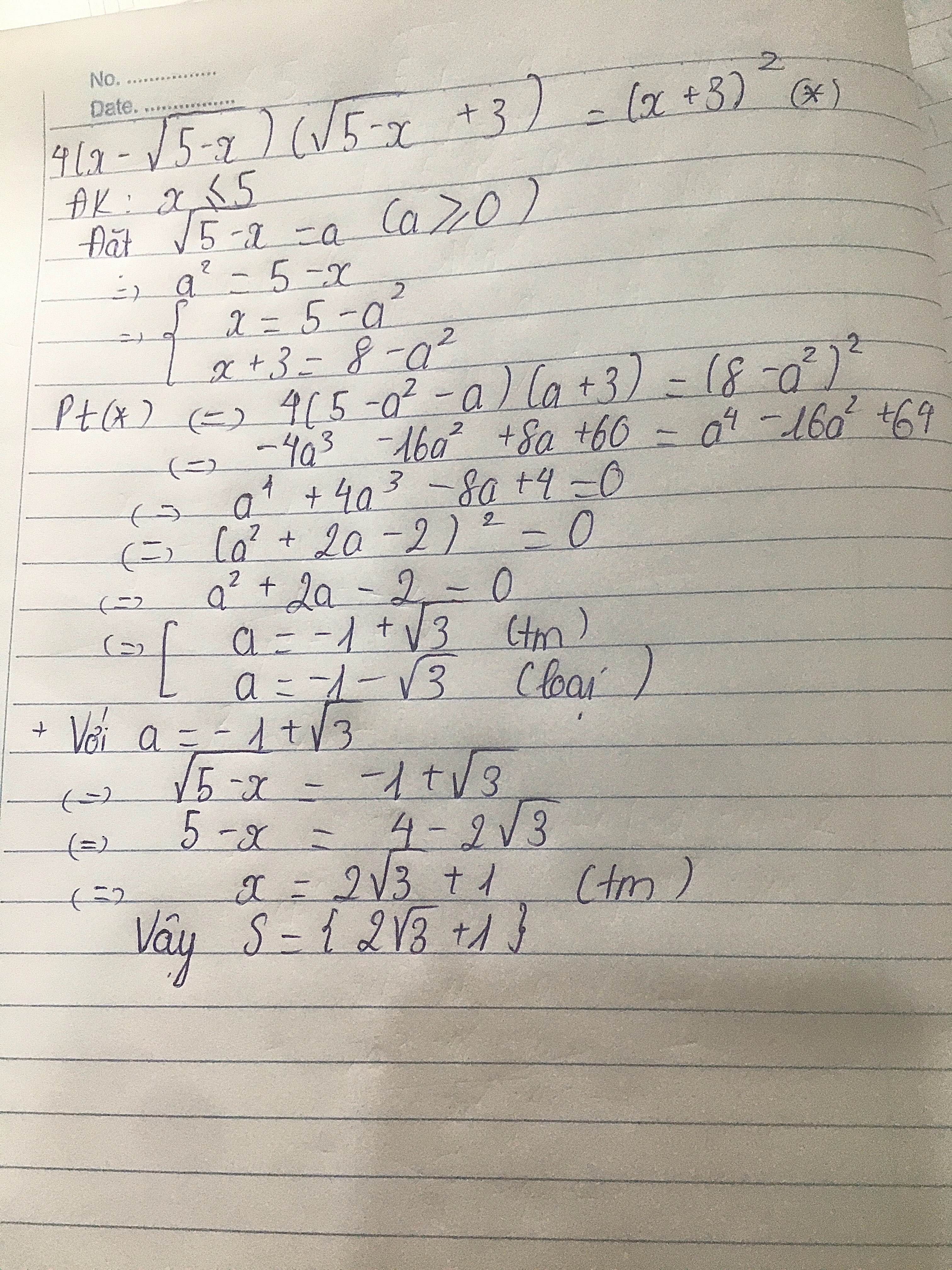
\(\left\{{}\begin{matrix}2\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)=\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\left(1\right)\\16x^5-20x^3+5\sqrt{xy}=\sqrt{\dfrac{y+1}{2}}\left(2\right)\end{matrix}\right.\).
ĐKXĐ: \(xy>0;y\ge-\dfrac{1}{2}\).
Nhận thấy nếu x < 0 thì y < 0. Suy ra VT của (1) âm, còn VP của (1) dương (vô lí)
Do đó x > 0 nên y > 0.
Với a, b > 0 ta có bất đẳng thức \(\left(a+b\right)^4\le8\left(a^4+b^4\right)\).
Thật vậy, áp dụng bất đẳng thức Cauchy - Schwarz ta có:
\(\left(a+b\right)^4\le\left[2\left(a^2+b^2\right)\right]^2=4\left(a^2+b^2\right)^2\le8\left(a^4+b^4\right)\).
Dấu "=" xảy ra khi và chỉ khi a = b.
Áp dụng bất đẳng thức trên ta có:
\(\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^4\le8\left[8\left(x^4+y^4\right)+16x^2y^2\right]=64\left(x^2+y^2\right)^2\)
\(\Rightarrow\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^2\le8\left(x^2+y^2\right)\). (3)
Lại có \(4\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)^2=4\left(\dfrac{x^6}{y^4}+2xy+\dfrac{y^6}{x^4}\right)\). (4)
Áp dụng bất đẳng thức AM - GM ta có \(\dfrac{x^6}{y^4}+xy+xy+xy+xy\ge5x^2;\dfrac{y^6}{x^4}+xy+xy+xy+xy\ge5y^2;3\left(x^2+y^2\right)\ge6xy\).
Cộng vế với vế của các bđt trên lại rồi tút gọn ta được \(\dfrac{x^6}{y^4}+2xy+\dfrac{y^6}{x^4}\ge2\left(x^2+y^2\right)\). (5)
Từ (3), (4), (5) suy ra \(4\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)^2\ge\left(\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\right)^2\Rightarrow2\left(\dfrac{x^3}{y^2}+\dfrac{y^3}{x^2}\right)\ge\sqrt[4]{8\left(x^4+y^4\right)}+2\sqrt{xy}\).
Do đó đẳng thức ở (1) xảy ra nên ta phải có x = y.
Thay x = y vào (2) ta được:
\(16x^5-20x^3+5x=\sqrt{\dfrac{x+1}{2}}\). (ĐK: \(x>0\))
PT này có một nghiệm là x = 1 mà sau đó không biết giải ntn :v
2 tháng 2 2021
\(\left\{{}\begin{matrix}\dfrac{x+2}{y-1}=\dfrac{x-4}{y+2}\\\dfrac{2x+3}{y-1}=\dfrac{4x+1}{2y+1}\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}\left(x+2\right)\left(y+2\right)=\left(y-1\right)\left(x-\text{4}\right)\\\left(2x+3\right)\left(2y+1\right)=\left(y-1\right)\left(4x+1\right)\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}xy+2x+2y+4=xy-4y-x+4\\4xy+2x+6y+3=4xy-4x+y-1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}3x+6y=0\\6x+5y=-4\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=-\dfrac{8}{7}\\y=\dfrac{4}{7}\end{matrix}\right.\)(TM)
2 tháng 2 2021
\(\left\{{}\begin{matrix}5\left(x-y\right)-3\left(2x+3y\right)=12\\3\left(x+2y\right)-4\left(x+2y\right)=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}5x-5y-6x-9y=12\\3x+6y-4x-8y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}-x-14y=12\\-x-2y=5\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=-\dfrac{26}{3}\\y=-\dfrac{7}{12}\end{matrix}\right.\)
Vậy HPT có nghiệm (x;y) = (\(-\dfrac{26}{3};-\dfrac{7}{12}\))
9 tháng 11 2023
Bài 1:
\(\sqrt{\left(4-\sqrt{5}\right)^2}+\sqrt{5+2\sqrt{5}+1}\)
\(=\left|4-\sqrt{5}\right|+\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(=4-\sqrt{5}+\sqrt{5}+1=5\)
Bài 2:
a: ĐKXĐ: x>=3
\(\sqrt{x-3}=6\)
=>x-3=36
=>x=36+3=39(nhận)
b: ĐKXĐ: \(x\in R\)
\(\sqrt{\left(x-3\right)^2}=12\)
=>\(\left|x-3\right|=12\)
=>\(\left[{}\begin{matrix}x-3=12\\x-3=-12\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=15\\x=-9\end{matrix}\right.\)
Bài 3:
a: \(P=\left(\dfrac{3-x\sqrt{x}}{3-\sqrt{x}}+\sqrt{x}\right)\cdot\left(\dfrac{3-\sqrt{x}}{3-x}\right)\)
\(=\dfrac{3-x\sqrt{x}+\sqrt{x}\left(3-\sqrt{x}\right)}{3-\sqrt{x}}\cdot\dfrac{3-\sqrt{x}}{3-x}\)
\(=\dfrac{3-x\sqrt{x}+3\sqrt{x}-x}{3-x}\)
\(=\dfrac{-\sqrt{x}\left(x-3\right)-\left(x-3\right)}{-\left(x-3\right)}=\dfrac{\left(x-3\right)\left(\sqrt{x}+1\right)}{x-3}=\sqrt{x}+1\)
b: \(P=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{1}{x+\sqrt{x}}\right):\dfrac{x-\sqrt{x}+1}{x\sqrt{x}+1}\)
\(=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\dfrac{x-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}+1}{1}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
c: \(A=\sqrt{3x-1}+3\cdot\sqrt{12x-4}-\sqrt{6^2\left(3x-1\right)}+\sqrt{5}\)
\(=\sqrt{3x-1}+6\sqrt{3x-1}-6\sqrt{3x-1}+\sqrt{5}\)
\(=\sqrt{3x-1}+\sqrt{5}\)
d: \(A=\left(\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}\right):\dfrac{a+2}{a-2}\)
\(=\left(\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}\right)\cdot\dfrac{a-2}{a+2}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}\cdot\dfrac{a-2}{a+2}\)
\(=\dfrac{2\left(a-2\right)}{a+2}\)
1 tháng 10 2021
Tham khảo:
1) Giải phương trình : \(11\sqrt{5-x}+8\sqrt{2x-1}=24+3\sqrt{\left(5-x\right)\left(2x-1\right)}\) - Hoc24