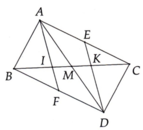
Cho tam giác ABC, I và K lần lượt là trung điểm của AB và AC. Chứng minh IK // BC, IK= \(\frac{1}{2}\)BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 8 2017
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
=
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu củ
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQMa A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc A
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
QM
1) Cho tam giác ABC, gọi I và K lần lượt là hình chiếu của A trên phân giác góc B và góc C. Cm: IK//BC
2) Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm AB, CD. Cm: MN < (AD+BC)/2
3) Cho tam giác ABC (AB<AC) trên AB lấy M, AC lấy N sao cho BM=CN. Gọi I và K lần lượt là trung điểm MN, BC. IK cắt AB, AC tại P, Q. Cm: góc BPM = góc AQM
tóm lị là ABGHMN là sai
30 tháng 8 2021
Xét tam giác ABC có
I là trung điểm của AB(gt)
K là trung điểm AC(gt)
=> IK là đường trung bình của tam giác ABC
30 tháng 8 2021
Xét ΔABC có
I là trung điểm của AB
K là trung điểm của AC
Do đó: IK là đường trung bình của ΔBAC
13 tháng 7 2023
a: Xét ΔABQ có IK//BQ
nen IK/QB=AI/AQ
Xét ΔAQC có IH//QC
nên IH/QC=AI/AQ
=>IK/QB=IH/QC
b,c,d: Cái đề này phải bổ sung thêm là Q là trung điểm của BC á nha bạn
F
18 tháng 7 2023
a,Xét tam giác ABQ có IK//BQ ( vì KH// BC)
=> `(IK)/(QB) = (AI)/(AQ)` (1)
Xét tam giác ACQ có IH//QC ( vì KH// BC)
=>`(IH)/(QC) = (AI)/(AQ)` (2)
Từ (1) và (2) => `(IK)/(QB) = (IH)/(QC)`
b,Xét tam giác EQC có IK//QC ( vì KH// BC)
=> `(IK)/(QC) = (IE)/(EQ)` (3)
CMTT => `(IH)/(BQ) = (IE)/(EQ)` (4)
Từ (3) và (4) => `(IH)/(BQ) = (IK)/(QC)`
c,Từ `(IK)/(QB) = (IH)/(QC)` và `(IH)/(BQ) = (IK)/(QC)`
=> `(IK)/(QB)` . `(IH)/(QB)` = `(IH)/(QC)` . `(IK)/(QC)`
=> `(IK . IH)/(QB . QB)` = `(IH . IK)/(QC .QC)`
=> `QB^2 = QC^2` => QB=QC
d, Từ QB=QC và `(IK)/(QB) = (IH)/(QC)` => IK=IH
28 tháng 5 2020
a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )