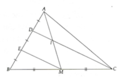
Cho tam giác ABC có: AM là trung tuyến, I là trung điểm của AM, CI cắt AB tại D , ME // CD ( E thuộc AB ). Chứng minh : a, AD=DE=EB b, DI/DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 10 2017
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI
27 tháng 7 2021
a) Xét ΔBCD có
M là trung điểm của BC
E là trung điểm của BD
Do đó: ME là đường trung bình của ΔBCD(Định nghĩa đường trung bình của tam giác)
Suy ra: ME//CD và \(ME=\dfrac{CD}{2}\)(Định lí 2 về đường trung bình của tam giác)
b) Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM(Định lí 1 về đường trung bình của tam giác)
c) Xét ΔAEM có
D là trung điểm của AE
I là trung điểm của AM
Do đó: DI là đường trung bình của ΔAEM
Suy ra: DI//EM và \(DI=\dfrac{EM}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: \(DI=\dfrac{EM}{2}\)(cmt)
nên \(EM=2\cdot DI\)
\(\Leftrightarrow\dfrac{DC}{2}=2\cdot DI\)
\(\Leftrightarrow DC=4\cdot DI\)
\(\Leftrightarrow DC-DI=4DI-DI\)
\(\Leftrightarrow CI=3DI\)
T
14 tháng 7 2019
Mình thử nhá, ko chắc.. bài này câu b, c có lẽ phải dùng kiến thức lớp 8 rồi. Bài gắt quá không biết có đánh máy sai chỗ nào không nữa
Ta chứng minh bổ đề sau: Trong tam giác, đoạn thẳng nối trung điểm hai cạnh thì song song với cạnh thứ ba và bằng nửa cạnh ấy (sẽ đăng sau)
Bây giờ bắt đầu giải:
a) Xét tam giác BCD có M là trung điểm BC, E là trung điểm BD
Suy ra EM // CD và EM = 1/2 CD (bổ đề bên trên)
b) Vẽ MF // AB suy ra MF // ED (do E và D thuộc AB) (1) và MF // AB (2) (F thuộc CD) từ câu a) EM//CD suy ra EM// DF (3)
Từ (1) và (3) suy ra tứ giác EMFD là hình bình hành. Do đó MF = DE. (4)
Từ (2) suy ra ^D1 = ^F1 (so le trong) (5)
Mặt khác từ MF // AD suy ra ^M1 = ^A1 (so le trong) (6)
Từ (4) và (5) và (6) suy ra tam giac DIA = tam giác FIM
Suy ra IA = IM hay I là trung điểm AM
c) Từ tam giác DIA = tam giác FIM
Suy ra DI = IF(7). Mặt khác từ câu A thì ME = 1/2 DC tức là DC = 2 ME.
Do đó ta cần chứng minh 4ID = 2ME tức là 2IF = ME (chia hai vế cho 2) hay IF + IF = ME (tách ra ở vế trái)
Từ (7) suy ra cần chức minh IF + ID = ME tức là FD = ME, điều này hiển nhiên đúng do câu b: tứ giác EMFD là hình bình hành.
VM
14 tháng 7 2019
Bạn tham khảo tại đây nhé nhưng không có câu c) đâu: https://hoc24.vn/hoi-dap/question/432305.html
Chúc bạn học tốt!
19 tháng 9 2021
a: Xét ΔBDC có
E là trung điểm của BD
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔBDC
Suy ra: EM//DC
b: Xét ΔAME có
E là trung điểm của AD
DI//EM
Do đó: I là trung điểm của AM
26 tháng 7 2019
Do ME là đường trung bình của tam giác BDC nên \(ME//DC\)
Mặt khác I là trung điểm của AM;\(DI//EM\Rightarrow DE=DA\)
Mà \(ME=ED\) vì E trung điểm.
Vậy \(AD=DE=EB\)
21 tháng 8 2019
Bổ sung chút cho bài của bạn Cood Kid
Gọi E là trung điểm BD
Xét tam giác BCD có M là trung điểm BC, E là trung điểm BD
=> ME là đường trung bình của tam giác BCD.
VM
5 tháng 10 2019
Vì \(AM\) là đường trung tuyến ứng với \(BC\left(gt\right)\)
=> \(MA=MB.\)
a) Nối \(E\) với \(M.\)
Xét \(\Delta BDC\) có:
\(\left\{{}\begin{matrix}DE=EB\left(gt\right)\\MA=MB\left(cmt\right)\end{matrix}\right.\)
=> \(ME\) là đường trung bình của \(\Delta BDC.\)
=> \(ME\) // \(CD\) (tính chất đường trung bình của tam giác)
Mà \(I\in CD\left(gt\right)\)
=> \(ME\) // \(ID.\)
Xét \(\Delta AEM\) có:
\(AD=AE\left(gt\right)\)
\(ME\) // \(ID\left(cmt\right)\)
=> \(I\) là trung điểm của \(AM\) (định lí đường trung bình của tam giác)
Chúc bạn học tốt!