Giải bất phương trình √x² + 61x ≤ 4x + 2 Giúp em với thanks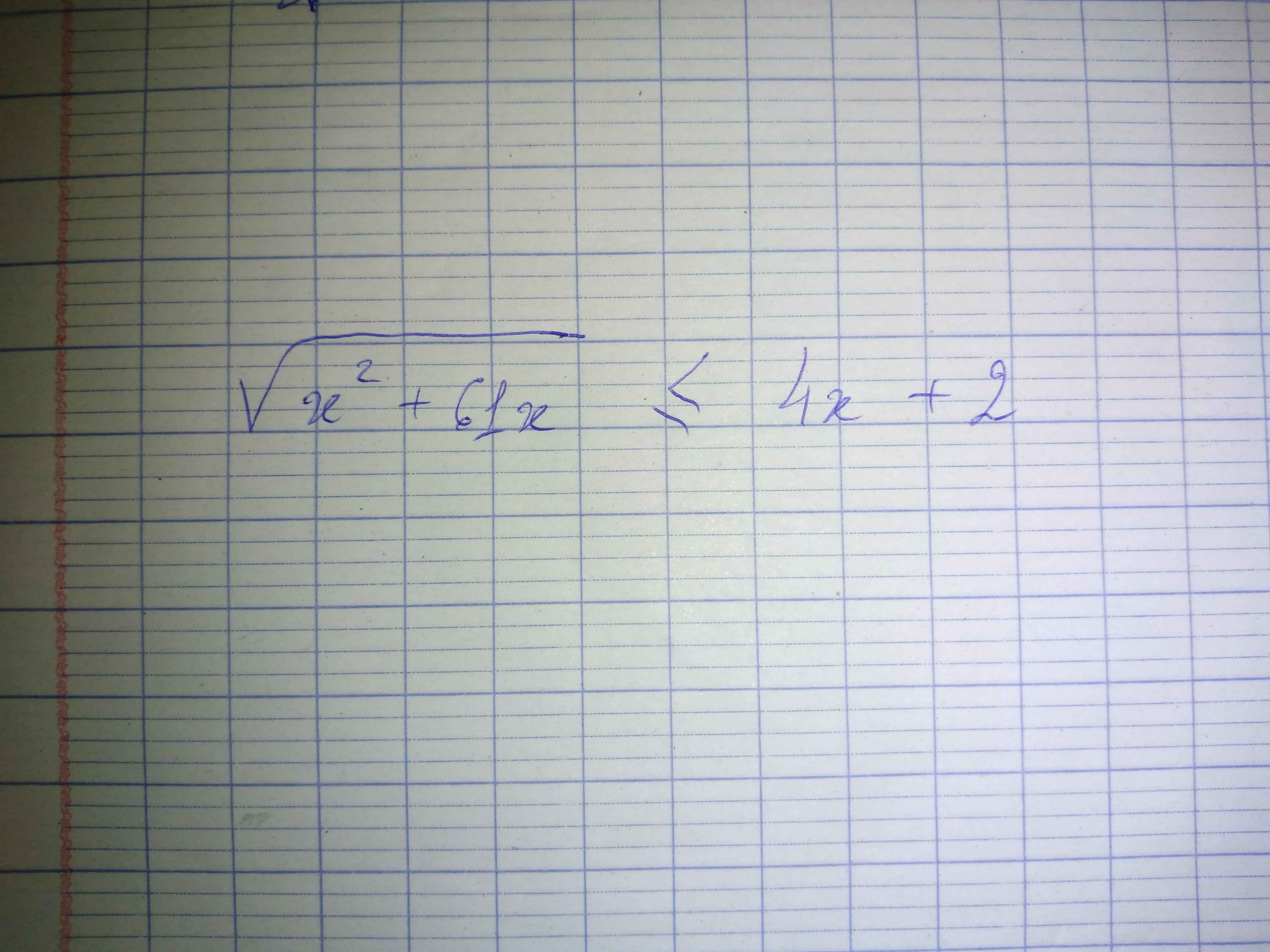
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HN
1
Những câu hỏi liên quan
HN
0
MT
1
4 tháng 10 2021
\(\left|4x-1\right|=5-x\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-1=5-x\left(x\ge\dfrac{1}{4}\right)\\4x-1=x-5\left(x< \dfrac{1}{4}\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{6}{5}\left(nhận\right)\\x=-\dfrac{4}{3}\left(nhận\right)\end{matrix}\right.\)
MK
0
TT
2
19 tháng 3 2019
\(\Leftrightarrow x\sqrt{2x-1}-4x+2=0\)0
\(\Leftrightarrow x\sqrt{2x-1}-2\left(2x-1\right)=0\)
\(\Leftrightarrow\sqrt{2x-1}\left(x-2\sqrt{2x-1}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{2x-1}=0\\x-2\sqrt{2x-1}=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{2}\\x=2\sqrt{2x-1}\left(1\right)\end{cases}}\)
+) giải phương trình (1) ta có
\(x=2\sqrt{2x-1}\)
\(\Leftrightarrow x^2=4.\left(2x-1\right)=0\)
\(\Leftrightarrow x^2-8x+4=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=4-2\sqrt{3}\\x=4+2\sqrt{3}\end{cases}}\)
Vậy phương trình đã cho có 3 nghiệm là \(x=\frac{1}{2};x=4+2\sqrt{3};x=4-2\sqrt{3}\)
BH
19 tháng 3 2019
Đặt \(\sqrt{2x-1}=t\Rightarrow t^2=2x-1\Rightarrow x=\frac{t^2+1}{2}\)
Vậy pt đã cho \(\Leftrightarrow\frac{t^2+1}{2}\cdot t=2t^2\\ \Leftrightarrow t^3+t-4t^2=0\Rightarrow t\left(t^2-4t+1\right)=0\)
\(t=0\Rightarrow x=\frac{1}{2}\left(tm\right)\)
\(t^2-4t+1=0\Rightarrow\orbr{\begin{cases}t=2-\sqrt{3}\\t=2+\sqrt{3}\end{cases}}\)
\(t=2-\sqrt{3}\Rightarrow2x-1=7-4\sqrt{3}\Rightarrow2x=8-4\sqrt{3}\\ \Rightarrow x=4-2\sqrt{3}\)
\(t=2+\sqrt{3}\Rightarrow2x-1=7+4\sqrt{3}\Rightarrow2x=8+4\sqrt{3}\\ \Rightarrow x=4+2\sqrt{3}\)
9 tháng 3 2023
Bài 2:
a: =>2x^2-4x+1=x^2+x+5
=>x^2-5x-4=0
=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)
b: =>11x^2-14x-12=3x^2+4x-7
=>8x^2-18x-5=0
=>x=5/2 hoặc x=-1/4
TT
1
KT
28 tháng 4 2018
Nếu \(x^2-9x+14=\left(x-7\right)\left(x-2\right)\ge0\)
\(\Leftrightarrow\)\(x\ge7;\)\(x\le2\)
thì \(\left|x^2-9x+14\right|=x^2-9x+14\)
Khi đó bpt trở thành: \(x^2-9x+14+3x>x^2-4\)
\(\Leftrightarrow\)\(-6x>-18\)
\(\Leftrightarrow\) \(x< 3\)(thỏa mãn)
Nếu \(x^2-9x+14=\left(x-7\right)\left(x-2\right)< 0\)
\(\Leftrightarrow\)\(2< x< 7\)
thì \(\left|x^2-9x+14\right|=-x^2+9x-14\)
Khi đó bpt trở thành: \(-x^2+9x-14+3x>x^2-4\)
\(\Leftrightarrow\)\(-2x^2+12x-10>0\)
\(\Leftrightarrow\) \(x^2-6x+5< 0\)
\(\Leftrightarrow\)\(\left(x-1\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\) \(1< x< 5\) (thỏa mãn)
Vậy...
PT
1
LS
0
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+61x\ge0\\4x+2\ge0\\x^2+61x\le\left(4x+2\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge0\\x\le-61\end{matrix}\right.\\x\ge-\dfrac{1}{2}\\15x^2-45x+4\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x\ge\dfrac{45+\sqrt{1785}}{30}\\x\le\dfrac{45-\sqrt{1785}}{30}\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}0\le x\le\dfrac{45-\sqrt{1785}}{30}\\x\ge\dfrac{45+\sqrt{1785}}{30}\end{matrix}\right.\)