Cho hình thang ABCD, AD//BC, AC cắt BD ở O. Xác định dạng của hình thang ABCD để SAOB lớn nhất ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ak cái này biết = 36
10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000%
tk nha

là 36 đó bạn mình khẳng định đúng 100 % vì mk gặp và thi rùi mà
đáy lớn hơn đáy bé: 15-12=3(cm) vậy chiều cao tam giác ADO hơn chiều cao tam giácBOC là 3(cm)
chiều cao tam giác BCO là: (15-3):2=6(cm)
S tam giác BOC là 12x6:2=36(cm2)

a: Xét ΔIBC và ΔIDA có
góc IBC=góc IDA
góc BIC=góc DIA
=>ΔIBC đồng dạng với ΔIDA
=>\(\dfrac{S_{IBC}}{S_{IDA}}=\left(\dfrac{IC}{IA}\right)^2=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
=>\(S_{IDA}=32\left(cm^2\right)\)
IC=1/2AI
=>\(S_{AIB}=2\cdot S_{BIC}=16\left(cm^2\right)\)
IA=2IC
=>\(S_{AID}=2\cdot S_{ICD}\)
=>\(S_{ICD}=16\left(cm^2\right)\)
=>\(S_{ABCD}=\)32+16+16+8=72cm2
b: ΔIBC đồng dạng với ΔIDA
=>IB/ID=IC/IA=1/2
=>BI=1/3BD
a: Xét ΔIBC và ΔIDA có
góc IBC=góc IDA
góc BIC=góc DIA
=>ΔIBC đồng dạng với ΔIDA
=>SIBCSIDA=(ICIA)2=(12)2=14��������=(����)2=(12)2=14
=>SIDA=32(cm2)����=32(��2)
IC=1/2AI
=>SAIB=2⋅SBIC=16(cm2)����=2⋅����=16(��2)
IA=2IC
=>SAID=2⋅SICD����=2⋅����
=>SICD=16(cm2)����=16(��2)
=>SABCD=�����=32+16+16+8=72cm2
b: ΔIBC đồng dạng với ΔIDA
=>IB/ID=IC/IA=1/2
=>BI=1/3BD

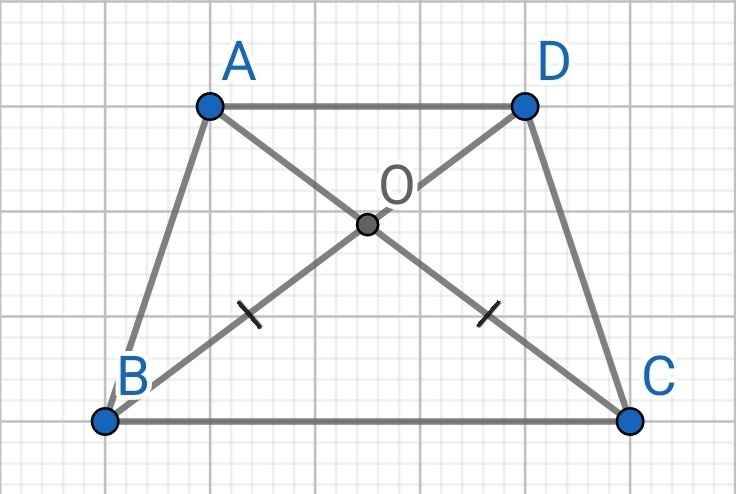 ∆OBC có:
∆OBC có:
OB = OC (gt)
⇒ ∆OBC cân tại O
⇒ ∠OBC = ∠OCB
Do ABCD là hình thang (AD // BC)
⇒ ∠OBC = ∠ODA (so le trong)
∠OCB = ∠OAD (so le trong)
Mà ∠OBC = ∠OCB (cmt)
⇒ ∠ODA = ∠OAD
∆OAD có:
∠ODA = ∠OAD (cmt)
⇒ ∆OAD cân tại O
⇒ OA = OD
Lại có:
OC = OB (gt)
⇒ OA + OC = OB + OD
⇒ AC = BD
⇒ ABCD là hình thang cân