Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

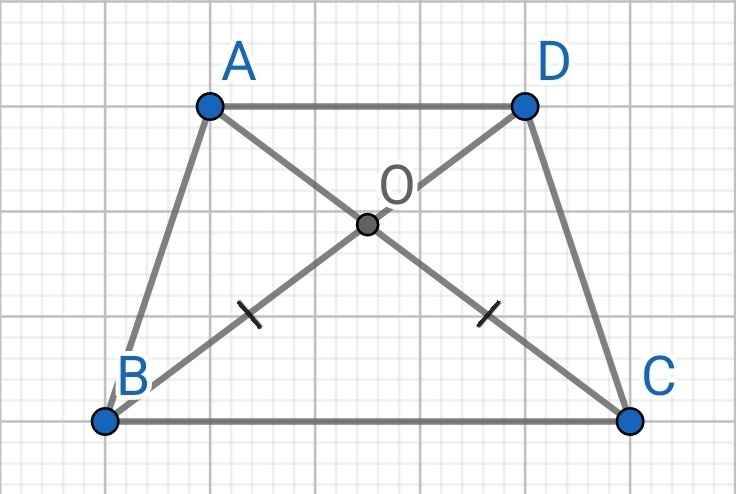 ∆OBC có:
∆OBC có:
OB = OC (gt)
⇒ ∆OBC cân tại O
⇒ ∠OBC = ∠OCB
Do ABCD là hình thang (AD // BC)
⇒ ∠OBC = ∠ODA (so le trong)
∠OCB = ∠OAD (so le trong)
Mà ∠OBC = ∠OCB (cmt)
⇒ ∠ODA = ∠OAD
∆OAD có:
∠ODA = ∠OAD (cmt)
⇒ ∆OAD cân tại O
⇒ OA = OD
Lại có:
OC = OB (gt)
⇒ OA + OC = OB + OD
⇒ AC = BD
⇒ ABCD là hình thang cân

Xét ΔDAB có OI//AB
nên \(\dfrac{OI}{AB}=\dfrac{DO}{DB}\)
Xét ΔBDC có OK//DC
nên \(\dfrac{OK}{CD}=\dfrac{BO}{BD}\)
=>\(\dfrac{OI}{AB}+\dfrac{OK}{CD}=\dfrac{BO}{BD}+\dfrac{DO}{DB}=1\)
Xét ΔADC có OI//DC
nên \(\dfrac{OI}{DC}=\dfrac{AI}{AD}\)
Xét ΔBDC có OK//DC
nên \(\dfrac{OK}{DC}=\dfrac{BK}{BC}\)
Xét hình thang ABCD có IK//AB//CD
nên \(\dfrac{AI}{AD}=\dfrac{BK}{BC}\)
=>\(\dfrac{OI}{DC}=\dfrac{OK}{DC}\)
=>OI=OK
=>\(\dfrac{OI}{AB}+\dfrac{OK}{CD}=\dfrac{OI}{AB}+\dfrac{OI}{CD}=1\)
