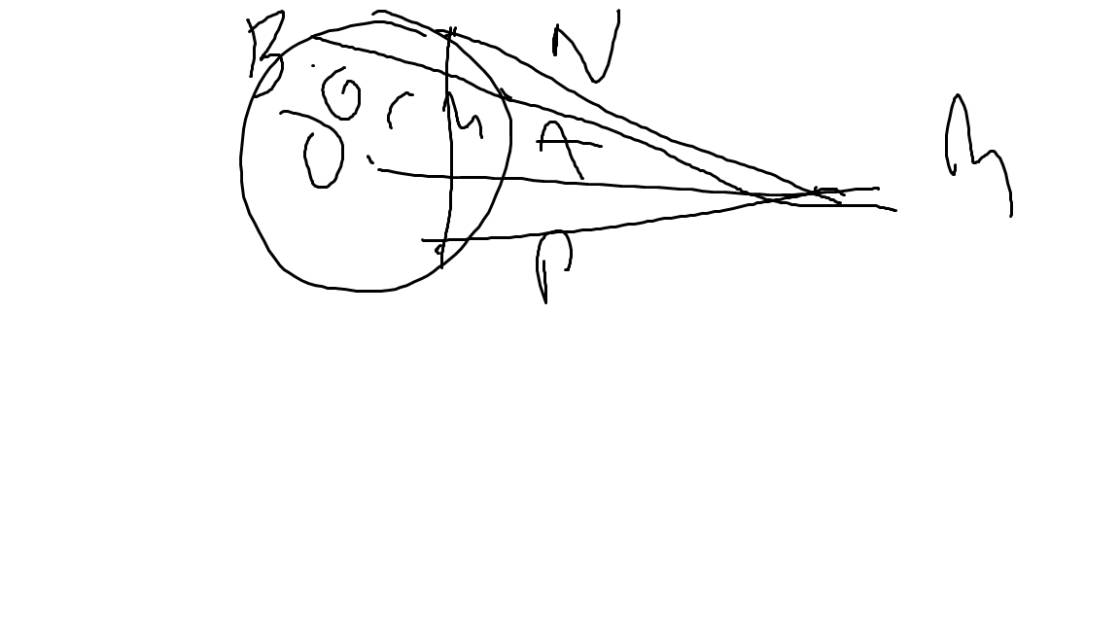
Từ một điểm M ở ngoài đường tròn (O;R) với OM > 2R vẽ hai tiếp tuyến MA, MB với (O) (A,B là tiếp điểm). Gọi I là trung điểm AM, BI cắt (O) tại C. Tia MC cắt (O) tại D và H là giao điểm của AB với OM.
a) Chứng minh tứ giác AOBM là tứ giác nội tiếp
b) Chứng minh AHC + AIC = 180
c) Chứng minh CA là tia phân giác của ICD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


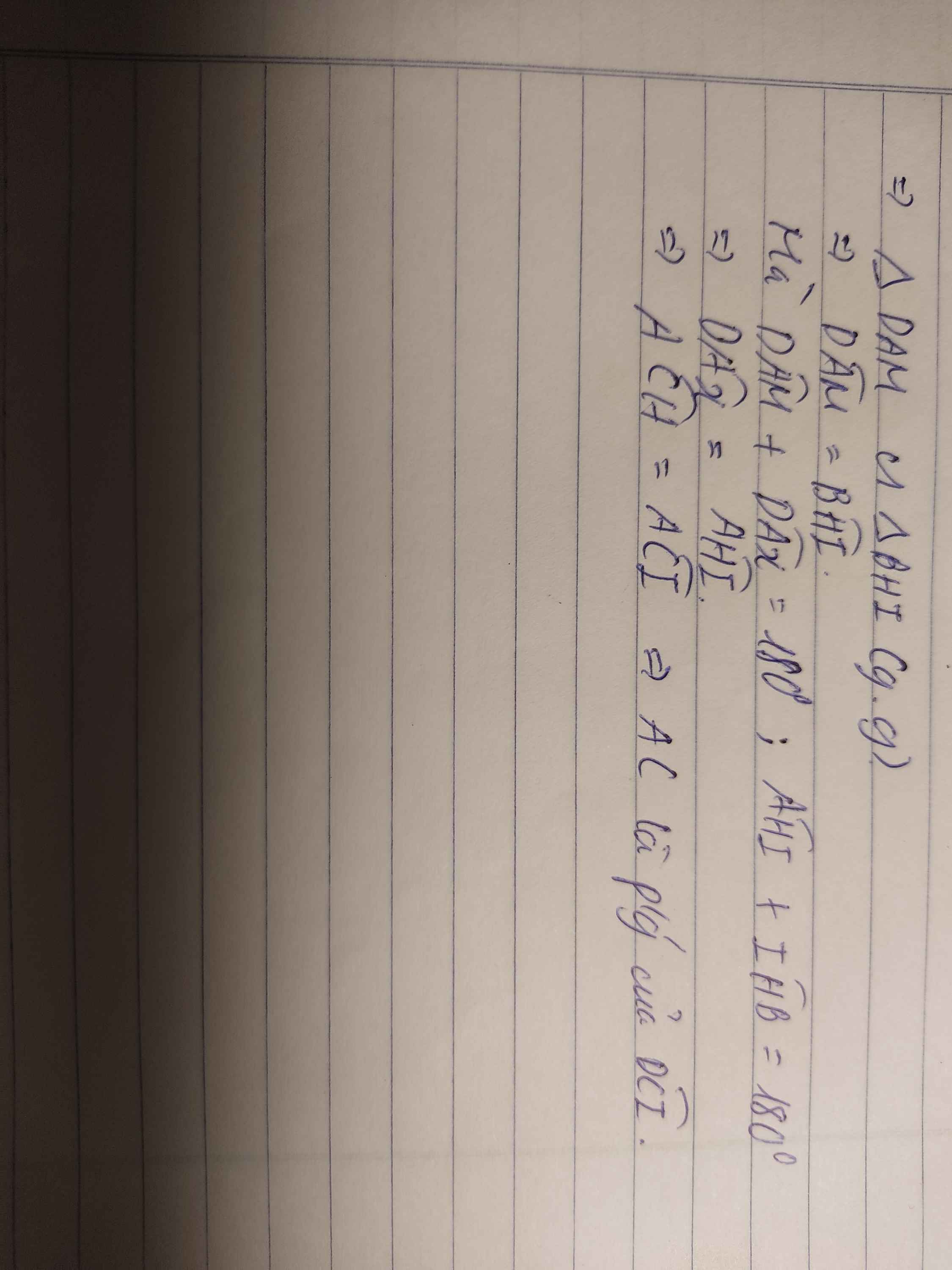

Trả lời :
Bn Nguyễn Tũn bảo dễ ẹt thì làm đi.
- Hok tốt !
^_^

Gọi bán kính của đường tròn (O) là R
Ta có:MB=MA+AB = MA + 2R
Suy ra: MA =MB – 2R
Ta lại có: M T 2 = MA.MB (cmt)
Suy ra: M T 2 = (MB- 2R).MB = M B 2 – 2R.MB
![]()

Xét tứ giác MIOK có
\(\widehat{MIO}+\widehat{MKO}=90^0+90^0=180^0\)
=>MIOK là tứ giác nội tiếp
=>M,I,O,K cùng thuộc một đường tròn
lấy A là trung điểm của OM,xét tam giác OMI có:
A là trung điểm của OM
O,M,I thuộc 1 đường tròn. (1)
Xét tam giác OMK có A là trung điểm của OM
O,M,K thuộc 1 đường tròn (2)
từ (1) và (2) suy ra 4 điểm M,I,O,K cùng thuộc 1 đường tròn

a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp đường tròn đường kính MO
Tâm là trung điểm của MO
Bán kính là MO/2
b: Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB
góc ABK=1/2*sđ cung AK=90 độ
=>AB vuông góc BK
=>BK//OM

a) Xét (O) có
AB là tiếp tuyến có B là tiếp điểm(gt)
AC là tiếp tuyến có C là tiếp điểm(gt)
Do đó: AB=AC(Tính chất hai tiếp tuyến cắt nhau)
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AB=AC(cmt)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
hay \(OA\perp BC\)(đpcm)
b) Xét tứ giác ABOC có
\(\widehat{OBA}\) và \(\widehat{OCA}\) là hai góc đối
\(\widehat{OBA}+\widehat{OCA}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
nên A,B,O,C cùng thuộc một đường tròn(đpcm)

M A B C 1
xét tam giác MCA và tam giác MAB có C1 = MAB ( 2 góc cùng chắn cung AB )
góc M chung
=> tam giác MCA đồng dạng tam giác MAB (g-g )
=> MA2 = MB.MC

xác định tâm rùi c/m tâm đó cách đều 4 điểm đó là đc
tâm là trung điểm của cạnh OA á

a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔAKM và ΔAMI có
góc AMK=góc AIM
góc MAK chung
=>ΔAKM đồng dạng với ΔAMI
=>AK/AM=AM/AI
=>AM^2=AI*AK
Xét ΔABM và ΔAMC có
góc AMB=góc ACM
góc BAM chung
=>ΔABM đồng dạng với ΔAMC
=>AB/AM=AM/AC
=>AM^2=AB*AC=AK*AI