Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,Trên nửa mặt phẳng bờ chứa tia OA có \(\widehat{AOB}=60^0< \widehat{AOC}=120^0\)
nên tia OB nằm giữa hai tia OA và OC
b, Vì tia OB nằm giữa hai tia OA và OC nên ta có :
\(\widehat{AOB}+\widehat{BOC}=\widehat{AOC}\)
Thay số : \(60^0+\widehat{BOC}=120^0\)
\(\Rightarrow\widehat{BOC}=120^0-60^0=60^0\)
Mà \(\hept{\begin{cases}\widehat{AOB}=60^0\\\widehat{BOC}=60^0\end{cases}\Rightarrow}\widehat{AOB}=\widehat{BOC}=60^0\)
Vì tia OB nằm giữa hai tia OA và OC
\(\widehat{AOB}=\widehat{BOC}=60^0\)
=> Tia OB là tia phân giác của góc \(\widehat{AOC}\)
c, Làm nốt

a) Trên cùng 1 nửa mp bờ chứa tia Oa có:
\(\widehat{aOb}< \widehat{aOc}\left(50^o< 100^o\right)\)
=> Ob nằm giữa Oa và Oc
Vậy Ob nằm giữa hai tia Oa và Oc
b) Vì Ob nằm giữa Oa và Oc nên:
\(\widehat{aOb}+\widehat{bOc}=\widehat{aOc}\)
=> 50o + \(\widehat{bOc}\) = 100o
hay \(\widehat{bOc}=100^o-50^o\)
\(\widehat{bOc}=50^o\)
Vậy \(\widehat{bOc}=50^o\)
c) Ta có: Ob nằm giữa Oa và Oc (1)
\(\widehat{aOb}=\widehat{bOc}\left(=50^o\right)\) (2)
Từ (1) và (2) suy ra Ob là tia phân giác của góc aOc
Vậy Ob là tia phân giác của \(\widehat{aOc}\)
a) Trên cùng một nữa mặt phẳng có bờ chưa tia Oa.
Có góc : aOb = 50o và aOc = 100o
=> Góc aOB < aOc
=> Tia Ob nằm giữa hai tia Oa và Oc.
b) Tia Ob nằm giữa hai tia Oa và Oc
=> aOb + bOc = aOc
=> 50 + bOc = 100
=> bOc = 100 - 50
=> bOc = 50o
Ta có tia Ob nằm giữa hai tia Oa và Oc
Và aOb = bOc = 50o
Vậy Ob là tia phân giác của góc aOc
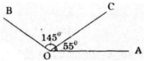

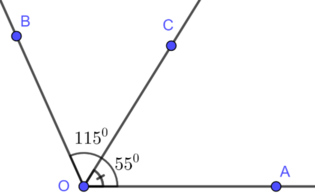

Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOb}< \widehat{aOc}\left(50^0< 135^0\right)\)
nên tia Ob nằm giữa hai tia Oa và Oc
\(\Leftrightarrow\widehat{aOb}+\widehat{bOc}=\widehat{aOc}\)
\(\Leftrightarrow\widehat{bOc}=135^0-50^0=85^0\)
Vậy: \(\widehat{bOc}=85^0\)
Trên một nửa mặt phẳng có bờ chứa tia Oa
Có: aÔb = 50o \(\Rightarrow\) aÔb < aÔc
aÔc = 135o \(\Rightarrow\) Tia Ob nằm giữa 2 tia Oa và Oc
\(\Rightarrow\) aÔb + bÔc = aÔc
50o + bÔc = 135o
bÔc = 135o - 50o
\(\Rightarrow\)bÔc = 85o