giúp mình giải vs vẽ hình nữa nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác AMBN có
I là trung điểm của AB
I là trung điểm của MN
Do đó: AMBN là hình bình hành

Diện tích của hình thang đó là:
( 8 + 12) x 5 : 2 = 50 (dm2)
Đ/s: 50 dm2
k mk nha bạn, thanks


a: Ta có: ΔCAB cân tại C
mà CM là đường trung tuyến
nên CM\(\perp\)AB
Ta có: M là trung điểm của BA
=>\(MB=MA=\dfrac{AB}{2}=1,5\left(m\right)\)
Xét ΔBCM có BI là phân giác
nên \(\dfrac{IC}{IM}=\dfrac{BC}{BM}=\dfrac{5}{1,5}=\dfrac{10}{3}\)
b: Xét ΔCBA có BD là phân giác
nên \(\dfrac{CD}{CB}=\dfrac{DA}{AB}\)
=>\(\dfrac{CD}{5}=\dfrac{DA}{3}\)
mà CD+DA=CA=5m
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{CD}{5}=\dfrac{DA}{3}=\dfrac{CD+DA}{5+3}=\dfrac{5}{8}\)
=>\(CD=\dfrac{25}{8}\left(m\right)\)
\(\dfrac{CD}{CB}=\dfrac{25}{8}:5=\dfrac{5}{8}\)



a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BH//CDvà BD//CH
BH//CD
AC vuông góc BH
Do đó: CA vuông góc CD
=>ΔCAD vuông tại C
CH//BD
CH vuông góc AB
Do đó: BD vuông góc AB
=>ΔABD vuông tại B
c: \(\widehat{ABD}=\widehat{ACD}=90^0\)
=>ABDC là tứ giác nội tiếp đường tròn đường kính AD
=>ABDC nội tiếp (I)
=>IA=IB=ID=IC



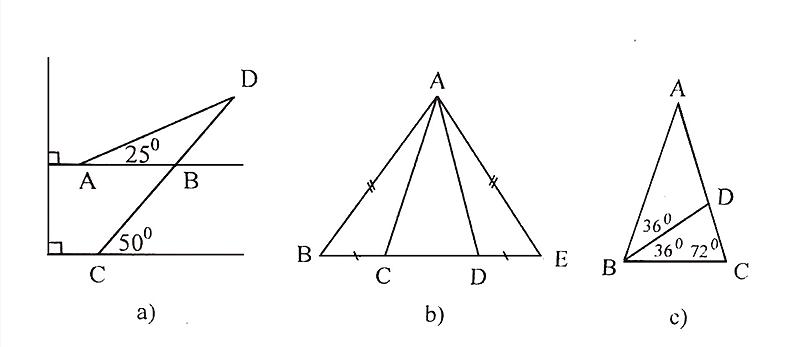
 Vẽ hình và giải chi tiết giúp mình nhé. Mình đang cần gấp.
Vẽ hình và giải chi tiết giúp mình nhé. Mình đang cần gấp.
a, Xét \(\Delta ABH\)và \(\Delta BCA\)có :
\(\widehat{B}\)chung
\(\widehat{BAC}=\widehat{BHA}\)
\(\Rightarrow\Delta ABH~\Delta BCA\)
b, Xét \(\Delta AKH\)và \(\Delta AHC\)có :
\(\widehat{KAH}\)chung
\(\widehat{AKH}=\widehat{AHC}=90^0\)
= > \(\Delta AKH~\Delta AHC\)
= > \(\frac{HK}{HC}=\frac{AH}{AC}\)( 1 )
Xét \(\Delta ABC\)có \(\widehat{A}=90^0\)
Áp dụng đinh lí Pytago trong tam giác ABC vuông tại A có :
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow6^2+8^2=BC^2\)
\(\Leftrightarrow100=BC^2\Rightarrow BC=\sqrt{100}=10\)
Xét \(\Delta ABC\)có : \(\widehat{A}-90^0\), \(AH\perp BC,H\in BC\)
\(\Rightarrow AH.BC=AB.AC\)
\(\Rightarrow AH.10=6.8\)
\(\Rightarrow AH=4,8\)
( 1 ) \(\Rightarrow\frac{HK}{HC}=\frac{AH}{AC}\Rightarrow\frac{HK}{6,4}=\frac{4,8}{8}\)
\(\Rightarrow HK=3,84\)
c, Bạn làm nốt nhé