Cho tam giác ABC, góc A=50 độ, góc B=80 độ. Tia Bx là tia đối của tia BA. Vẽ tia Bt là tia phân giác của Góc xBC. Chứng tỏ rằng tia Bt song song vs tia AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 6 2015
a) có lẽ đề sai. góc xBz phải là 160 độ hoặc góc xAy=70
vì muốn c/m Bt // Ay. ta chững minh góc xBt=góc xAy ( vị trí đồng vị)
Bt là phân giác => góc xBt=1/2 góc xBz => góc xAy=góc xBt=1/2 góc xBz
mà 80 thì không thể =1/2 của 140 đc => đề sai ở một hoặc hai dữ kiện góc
b) góc CBA kề bù với góc xBz => CBA=180-xBz ( sửa đề xong rồi tính nha)
dựa vào định lí tổng ba góc. tam giác ABC: góc A+góc CBA+ góc ACB=180 => ACB=180-xAy-CBA
sửa lỗi của đề rồi ghép vào là xong nha
26 tháng 7 2023
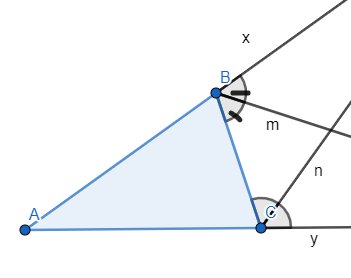
a) Giả sử Bm // Cn. Khi đó ta có:
\(\widehat{xBm}=\widehat{BCn}\) (hai góc đồng vị) và \(\widehat{BCn}+\widehat{CBm}=180^o\) (hai góc trong cùng phía)
\(\Rightarrow\widehat{xBm}+\widehat{mBC}=\widehat{xBC}=180^o\) (a)
Mà \(\widehat{ABC}\) và \(\widehat{xBC}\) là hai góc kề bù (vì \(\widehat{xBC}\) là góc ngoài đỉnh B)
\(\Rightarrow\widehat{ABC}+\widehat{mBC}=180^o\)
\(\Rightarrow\widehat{mBC}=180^o-\widehat{ABC}\)
\(\Rightarrow\widehat{mBC}< 180^o\) (b)
Từ (a) và (b) suy ra vô lí, suy ra Bm không song song với Cn
Vậy Bm cắt Cn
HN
2 tháng 8 2016
Xét \(\Delta ABC\) có:
\(\widehat{BAC} + \widehat{B} + \widehat{C} = 180^O\)(Tổng 3 góc của 1 tam giác)
\(80^O + 50^O + \widehat{C} = 180^O\)\((\widehat{BAC} = 80^O(gt); \widehat{B} = 50^O(gt))\)
\(\widehat{C} = 180^O - 80^O - 50^O = 50^O\)
\(\widehat{DAB} = \widehat{B} + \widehat{C}\)(\(\widehat{DAB}\) là góc ngoài tại đỉnh A của \(\Delta ABC\))
\(\widehat{DAB} = 50^O + 50^O = 100^O\)
\(\widehat{DAm} = \frac{1}{2} \widehat{DAB}\)(Am là tia phân giác của \(\widehat {DAB} \) (gt))
\(\widehat{DAm} = \frac{1}{2} . 100^O = 50^O\)
\(\Rightarrow\)\(\widehat{DAm} = \widehat{ADE}\)
mà 2 góc này nằm ở vị trí so le trong
\(\Rightarrow\)\(DE//AM (dpcm)\)
b) Ta có:
\(DE//AM (cmt)\)
\(DE//BC\) (2 góc so le trong)
\(\Rightarrow\)\(BC//AM\)(định lí 3 trong bài từ vuông góc đến song song)