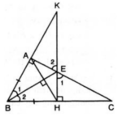
Cho tam giác ABC vuông tại A. đường phân giác BE. Kẻ EH vuông góc với BC. gọi K là giao điểm của AB và HE. Chứng minh rằng :
- ΔABE = ΔHBE
- BE là đường trung trực của AH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 10 2019
ΔABE = Δ HBE
⇒ BA = BH, EA = EH (các cặp cạnh tương ứng)
⇒ E, B cùng thuộc trung trực của AH
nên đường thẳng EB là trung trực của AH.
4 tháng 3 2022
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔABE=ΔHBE
b: Ta có:ΔABE=ΔHBE
nên BA=BH và EA=EH
=>BE là đường trung trực của AH
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: EK=EC
hay ΔEKC cân tại E
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC
CM
16 tháng 5 2017
Xét ΔABE vuông tại A và ΔHBE vuông tại H có :
BE chung
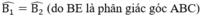
⇒ ΔABE = ΔHBE (cạnh huyền – góc nhọn)
28 tháng 10 2023
1. ΔABE = ΔHBE
Xét ΔABE và ΔHBE, ta có :
BE là cạnh chung.
=> ΔABE = ΔHBE
2. BE là đường trung trực của AH :
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
3. EK = EC
Xét ΔKAE và ΔCHE, ta có :
EA = EH (cmt)
=> ΔKAE và ΔCHE
=> EK = EC
4. EC > AC
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.
28 tháng 7 2023
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔABE=ΔHBE
b: ΔBAE=ΔBHE
=>BA=BH và EA=EH
=>BE là trung trực của AH
c: Xét ΔEAK vuông tại A và ΔEHC vuông tại H có
EA=EH
góc AEK=góc HEC
=>ΔEAK=ΔEHC
=>EK=EC
=>ΔEKC cân tại E
14 tháng 7 2021
a) Xét hai tam giác vuông ΔABE và ΔHBE có:
∠ABE = ∠HBE (BE là tia phân giác giả thiết)
BE cạnh chung
⇒ ΔABE = ΔHBE (cạnh huyền - góc nhọn)
Vậy ΔABE = ΔHBE
b) AB = HB (2 cạnh tương ứng)
⇒ B thuộc đường trung trực của đoạn AH (1)
AE=HE (2 cạnh tương ứng)
⇒ E thuộc đường trung trực của đoạn AH (2)
Từ (1) và (2) ⇒ BE là đường trung trực của đoạn AH
Vậy BE là đường trung trực của đoạn AH
c) Xét hai tam giác vuông ΔAEK và ΔHEC có:
∠AEK = ∠HEC (đối đỉnh)
AE = HE (cmt)
⇒ ΔAEK = ΔHEC (cạnh góc vuông - góc nhọn)
⇒ EK = EC (2 cạnh tương ứng) (3)
Vậy EK = EC
d) Ta có: ΔAEK vuông tại A
⇒ ∠K<∠A
⇒ AE<KE (4)
Từ (3) và (4) ⇒ AE<EC
Vậy AE<EC
14 tháng 7 2021
a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(Cạnh huyền-góc nhọn)
b) Ta có: ΔABE=ΔHBE(cmt)
nên BA=BH(Hai cạnh tương ứng) và EA=EH(hai cạnh tương ứng)
Ta có: BA=BH(cmt)
nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: EA=EH(cmt)
nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra BE là đường trung trực của AH
29 tháng 7 2016
1. ΔABE = ΔHBE
Xét ΔABE và ΔHBE, ta có :
BE là cạnh chung.
=> ΔABE = ΔHBE
2. BE là đường trung trực của AH :
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
3. EK = EC
Xét ΔKAE và ΔCHE, ta có :
EA = EH (cmt)
=> ΔKAE và ΔCHE
=> EK = EC
4. EC > AC
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.
TN
20 tháng 8 2015
a) xet tam giac ABE vuong tai A va tam giac HBE vuong tai H ta co
BE=BE ( canh chung) ; goc ABE= goc HBE ( BE la tia p/g goc B)
--> tam giac ABE= tam giac HBE ( ch=gn)
b) ta co
BA=BH ( tam giac ABE= tam giac HBE)
EA=EH( tam giac ABE= tam giac HBE)
==> BE la duong trung truc cua AH
c) xet tam giac EKA va tam giac ECH ta co
AE=EH ( tam giacABE= tam giacHBE) ; goc EAK= goc EHC (=90); goc AEK= goc HEC ( 2 goc doi dinh )
--> tam giac EKA = tam giac ECH ( g--c-g)
--> EK=EC (2 canh tuong ung )
d) tu diem E den duong thang HC ta co :
EH la duong vuong goc ( EH vuong goc BC)
EC la duong xien
-> EH<EC ( quan he duong xien duong vuong goc)
ma EH= AE ( tam giac ABE= tam giac HBE)
nen AE < EC
3 tháng 5 2017
Cho tam giác ABC vuông tại a ; đường phân giác BE. kẻ EH cuông góc BC(H thuộc BC) Gọi K là giao điểm của AB và HE . Chứng minh rằng
1) Tam giác ABE=tam giác HBE
2) BE là đường trung trực của đoạn thẳng AH; Chứng minh BE vuông góc KC
3) AE<EC
19 tháng 6 2023
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>AE=HE
c: BA=BH
EA=EH
=>BE là trung trực của AH
d: BE là trung trực của AH
=>BE vuông góc AH
1. ΔABE = ΔHBE
Xét ΔABE và ΔHBE, ta có :
ABE = HBE (gt)
BE là cạnh chung
=> ΔABE = ΔHBE (cạnh huyền - góc nhọn)
2. BE là đường trung trực của AH :
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .