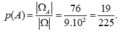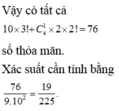Tìm tất cả các số tự nhiên n sao cho n4 là một số gồm 7 chữ số và n4 chia hết cho 2401
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
1 tháng 3 2021
1) n4 + 4 = (n4 + 4n2 + 4) - 4n2 = (n2 + 2)2 - (2n)2 = (n2 + 2 + 2n).(n2 + 2 - 2n)
Ta có n2 + 2n + 2 = (n+1)2 + 1 > 1 với n là số tự nhiên
n2 - 2n + 2 = (n -1)2 + 1 1 với n là số tự nhiên
Để n4 + 4 là số nguyên tố => thì n4 + 4 chỉ có 2 ước là chính nó và 1
=> n2 + 2n + 2 = n4 + 4 và n2 - 2n + 2 = (n -1)2 + 1 = 1
(n -1)2 + 1 = 1 => n - 1= 0 => n = 1
Vậy n = 1 thì n4 là số nguyên tố
CM
21 tháng 5 2018
Chọn A
+) Không gian mẫu Ω = “Chọn ngẫu nhiên một số trong các số tự nhiên có 3 chữ số”.=> | Ω | = 9. 10 2
+) Biến cố A = “Số tự nhiên được chọn chia hết cho 9 và các chữ số đôi một khác nhau”.
Ta tìm số các số tự nhiên gồm 3 chữ số khác nhau và chia hết cho 9 (tổng các chữ số là một số chia hết cho 9).
Bộ ba số (a;b;c) với a,b,c ∈ [0;9](a,b,c đôi một khác nhau ) và a + b + c = 9m, m ∈ ℕ * được liệt kê dưới đây:
Vậy có tất cả 10.3! + 4.2.2! = 76 => | Ω A | = 76
Xác suất cần tính bằng 