\(\int\limits^{\dfrac{\pi}{2}}_{\dfrac{\pi}{3}}\dfrac{1+sinx}{1+cosx}e^xdx\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 6 2021
\(\int\limits^{\dfrac{\pi}{2}}_0sinxdx=cosx|^{\dfrac{\pi}{2}}_0=-1\)

DL
20 tháng 2 2021
Câu nào mình biết thì mình làm nha.
1) Đổi thành \(\dfrac{y^4}{4}+y^3-2y\) rồi thế số.KQ là \(\dfrac{-3}{4}\)
2) Biến đổi thành \(\dfrac{t^2}{2}+2\sqrt{t}+\dfrac{1}{t}\) và thế số.KQ là \(\dfrac{35}{4}\)
3) Biến đổi thành 2sinx + cos(2x)/2 và thế số.KQ là 1

LN
1 tháng 4 2017
a) =
=
b) =
=
=
c)=
d)=
=
e)=
=
g)Ta có f(x) = sin3xcos5x là hàm số lẻ.
Vì f(-x) = sin(-3x)cos(-5x) = -sin3xcos5x = f(-x) nên:

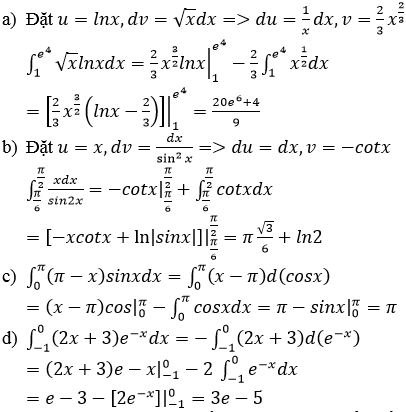
Ok bat ong doi lau roi
\(\int\dfrac{1+\sin x}{1+\cos x}e^xdx=\int\dfrac{e^xdx}{1+\cos x}+\int\dfrac{e^x\sin x}{1+\cos x}dx\)
\(I_1=\int\dfrac{e^xdx}{1+\cos x}\)
\(I_2=\int\dfrac{e^x\sin x}{1+\cos x}dx\)
\(\left\{{}\begin{matrix}u=\dfrac{\sin x}{1+\cos x}\\dv=e^xdx\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}du=\dfrac{\cos x\left(1+\cos x\right)+\sin^2x}{\left(1+\cos x\right)^2}dx=\dfrac{dx}{1+\cos x}\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I_2=\dfrac{e^x.\sin x}{1+\cos x}-\int\dfrac{e^xdx}{1+\cos x}=\dfrac{e^x\sin x}{1+\cos x}-I_1\)
\(\Rightarrow I=\dfrac{e^x\sin x}{1+\cos x}\)
P/s: Done, ông thay cận vô nhé :)