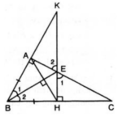
Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt cạnh AC tại E. Từ E kẻ EH vuông góc BC tại H. a) Chứng minh rằng: ΔABE = ΔHBE b) Chứng minh rằng: BE là đường trung trực của AH c) Gọi giao điểm của AB và EH là K. Xác định dạng của tam giác ECK d) Chứng minh rằng: AH // CK e) Tìm điều kiện của ΔABC để ∠AEB = ∠HEC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác BHA và BHE có:
BD chung
ˆABD^=ˆEBD^(vì BD là phân giác ˆBB^)
ˆBHA^=ˆBHE^(vì AH vuông góc với Bd tại H)
⇒Tam giác BHA=tam giac BHE(c.g.v-g.n.k)
b) Xét Tam giác BDA và tam giác BDE có
BD chung
BA=BE( vì tam giac BHA = tam giac BHE( chứng minh phần a))
ABD=EBD( vì BD là phân giác củaˆBB^)
⇒⇒Tam giác BDA = Tam giác BDE(c.g.c)
⇒⇒ˆBEA^=ˆA^= 90o(2 canh tương ứng và ˆA^= 90o)
ED vuông góc với B tại E
c, AD = DE
DE < CD do tam giác CDE vuông tại E
=> AD < DC
d, DA= DE do tam giác ABD = tam giác EBD (Câu b)
=> tam giác DAE cân tại D (đn)
=> ^DAE = ^DEA (tc) (1)
có : AK _|_ BC (gt) ; DE _|_ BC (câu b)
=> DE // AK
=> ^DEA = ^EAK (slt) và (1)
=> ^DAE = ^EAK mà AE nằm giữa AD và AK
=> AE là phân giác của ^CAK (đpcm)
a) Vì EH ⊥ BC ( gt )
=> ΔBHE vuông tại H
Xét tam giác vuông BAE và tam giác vuông BHE có :
BE chung
∠B1 = ∠B2 ( BE là tia phân giác của ∠BAC )
=> ΔBAE = ΔBHE ( cạnh huyền - góc nhọn )
b) Gọi I là giao điểm của AH và BE
Xét ΔABI và ΔHBI có :
BA = BH (ΔBAE = ΔBHE (cmt)
∠B1 = ∠B2 ( BE là tia phân giác của ∠BAC )
BI chung
=> ΔABI = ΔHBI ( c.g.c )
=> ∠AIB = ∠AIH ( 2 góc tương ứng )
Mà ∠AIB + ∠AIH = 1800 ( 2 góc kề bù )
=> ∠AIB = ∠AIH = 900
=> BI ⊥ AH (1)
Ta có: IA = IH ( ΔABI = ΔHBI ( cmt )
Mà I nằm giữa hai điểm A và H (2)
=> I là trung điểm của AH ( 3)
Từ (1) (2) (3) => BI là trung trực của AH
Hay BE là trung trực của AH
c) Xét ΔKAE và ΔCHE có:
∠KAE = ∠CHE ( = 900 )
AE = HE ( ΔBAE = ΔBHE (cmt)
∠AEK = ∠HEC ( 2 góc đối đỉnh )
=> ΔKAE = ΔCHE ( g.c.g )
=> EK = EC ( 2 cạnh tương ứng )

1. ΔABE = ΔHBE
Xét ΔABE và ΔHBE, ta có :
ABE = HBE (gt)
BE là cạnh chung
=> ΔABE = ΔHBE (cạnh huyền - góc nhọn)
2. BE là đường trung trực của AH :
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .

Xét ΔABE vuông tại A và ΔHBE vuông tại H có :
BE chung
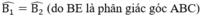
⇒ ΔABE = ΔHBE (cạnh huyền – góc nhọn)

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
góc ABE=góc DBE
=>ΔBAE=ΔBDE
b: BA=BD
EA=ED
=>BE là trung trực của AD
c: góc BAD+góc CAD=90 độ
góc HAD+góc BDA+90 độ
góc BAD=góc BDA
=>góc CAD=góc HAD
=>AD làphân giác của góc HAC

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D

Bài 4: a) Xét ABE vàHBE có:
BE chung
ABE= EBH (vì BE là phân giác)
=> ABE=HBE (cạnh huyền- góc nhọn)
b, Vì ABE=HBE(cmt)
=> BA = BH và EA = EH
=> điểm B, E cách đều 2 mút của đoạn thẳng AH
=>BE là đường trung trực của đoạn thẳng AH
c, Vì AC vuông góc BK => EAK = \(90\) độ
EH vuông góc BC => EHC = 90 độ
Xét AEK vàHEC có:
EAK = EHC (= 90độ)(cmt)
AE = EH (cmt)
AEK = HEC (đối đỉnh)
=> AEK HEC (g.c.g)
=> EK = EC (2 cạnh tương ứng)
Xét HEC vuông tại H (vì EHC = 90 độ )
có EH < EC(cạnh huyền lớn hơn cạnh góc vuông)
Mà AE = EH (cmt) => AE < EC

Bạn tự vẽ hình nha!!!
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.

e) vì AC vuông góc vs BK , KE ( kéo dài ED)vuông góc với BC mà AC và KE cắt nhau tại D => D là trực tâm của tam giác KBC => BD vuoogn góc với KC ( 1 ) .M là trung điểm của KC => BM là đường cao đồng thời là đường trung trực của tam giác KBC ( 2 ) . từ ( 1 ) và ( 2 ) => B, D , M thằng hàng
a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔABE=ΔHBE
b: Ta có:ΔABE=ΔHBE
nên BA=BH và EA=EH
=>BE là đường trung trực của AH
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: EK=EC
hay ΔEKC cân tại E
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC