Cho △ABC có BC= 5cm, AC= 4cm, AB= 6cm và AD là đường phân giác. Tính tỉ số diện tích của hai tam giác ABD và ACD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 4 2022
\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{4}{8}=\dfrac{1}{2}\)
H
21 tháng 2 2018
a, Theo tính chất đường phân giác ta có : \(\frac{AD}{AB}=\frac{DC}{BC}\)=> \(\frac{AD}{4}=\frac{DC}{6}\)=> \(\frac{AD}{2}=\frac{DC}{3}=\frac{AD+DC}{2+3}=\frac{AC}{5}=\frac{5}{5}=1\)
=> \(\hept{\begin{cases}AD=2\\DC=3\end{cases}}\)
21 tháng 2 2018
a) Áp dụng tính chất đường phân giác ta có:
\(\frac{AD}{CD}=\frac{AB}{BC}=\frac{4}{6}=\frac{2}{3}\)
\(\Leftrightarrow\frac{AD}{2}=\frac{AB}{3}=\frac{AD+AB}{2+3}=1\)
\(\Leftrightarrow AD=2;AB=3\)
CM
1 tháng 3 2017
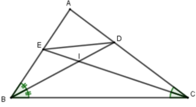
Ta có: A D A B = D C B C (t/c)
⇒ A D 4 = D C 6 = A D + D C 4 + 6 = 5 10 = 1 2
=> AD = 4. 1 2 = 2, DC = 6. 1 2 = 3
Suy ra:
D I I B = D C C B = 3 6 = 1 2 ⇒ D I D B = 1 3 B E E A = B C A C = 6 5 ⇒ B E B A = 6 11 A D D C = 2 3 ⇒ A D A C = 2 5
Suy ra S D I E = 1 3 S B D E
⇒ S D I E = 1 3 . 6 11 . 2 5 = 4 55 S A B C
Vậy S D I E S A B C = 4 55
Đáp án: A
23 tháng 1 2021
a) △ABC có AD là đường phân giác
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{DB}{DC}\) (t/c)
\(\Rightarrow\dfrac{DB}{DC}=\dfrac{6}{9}=\dfrac{2}{3}\Rightarrow3DB=2DC\)
Mà \(BD+CD=BC=10\)
\(\Rightarrow2BD+2CD=5BD=20\\ \Rightarrow BD=4\left(cm\right)\)
△ABC có AE là đường phân giác ngoài tại đỉnh A
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{EB}{EC}\) (T/c)
\(\Rightarrow\dfrac{EB}{EC}=\dfrac{6}{9}=\dfrac{2}{3}\Rightarrow3EB=2EC\)
Mà \(EC=EB+BC=EB+10\)
\(\Rightarrow2EB+20=2EC=3EB\\ \Rightarrow BE=20\left(cm\right)\)
b) △ABC có AD là đường phân giác trong
AE là đường phân giác ngoài tại đỉnh A
\(\Rightarrow AD\perp AE\) → △ADE vuông tại A
c) Kẻ AH ⊥ BC
\(S_{ADB}=\dfrac{AH}{2}\cdot BD\)
\(S_{ADC}=\dfrac{AH}{2}\cdot CD\)
Mà \(DB=\dfrac{2}{3}DC\)
\(\Rightarrow S_{ADB}=\dfrac{2}{3}S_{ADC}\)
Gọi đường cao chung của 2 tam giác ABD và ACD là AH
Xét tam giác ABC có:
AD là đường phân giác
=>\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)
=>\(\dfrac{DB}{DB+DC}=\dfrac{AB}{AB+AC}\)
=>\(\dfrac{DB}{BC}=\dfrac{6}{6+4}\)
=>\(\dfrac{DB}{5}=\dfrac{6}{10}\)
=>DB=3cm
CMTT:DC=2cm
Ta có:\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{\dfrac{1}{2}.AH.BD}{\dfrac{1}{2}.AH.DC}=\dfrac{BD}{DC}=\dfrac{3}{2}\)
-Xét △ABC có: AD là đường phân giác (gt).
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{6}{4}=\dfrac{3}{2}\) (định lí đường phân giác).
\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{DB}{DC}=\dfrac{3}{2}\)