1 thửa ruộng hình chữ nhật có chiều dài hơn chiều rộng 5m . nếu giảm cả chiều dài và chiều rộng đi 3m thì diện tích thửa đất sẽ giảm đi 42 m . tính diện tích thửa ruộng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VD
13 tháng 8 2018
Diện tích thửa đất sẽ giảm đi 42 m2. Chính là diện tích hai hình chữ nhật (H1) màu vàng và một hình chữ nhật (H2) màu đen.
Hình chữ nhật (H2) có chiều dài là 3m và chiều rộng là : (5 – 3 = 2m)
Diện tích hình chữ nhật (H2) :
3 x 2 = 6m2
Diện tích hình chữ nhật (H1) :
(42 – 6 ) : 2 = 18 m2
Chiều rộng hình chữ nhật ban đầu :
18 : 3 = 6m
Chiều dài hình chữ nhật ban đầu :
6 + 5 = 11m
Vậy diện tích thửa đất lúc ban đầu :
6 x 11 = 66 m2
BD
13 tháng 8 2018
Diện tích thửa đất sẽ giảm đi 42 m2. Chính là diện tích hai hình chữ nhật ﴾H1﴿ màu vàng và một hình chữ nhật ﴾H2﴿ màu đen.
Hình chữ nhật ﴾H2﴿ có chiều dài là 3m và chiều rộng là : ﴾5 – 3 = 2m﴿
Diện tích hình chữ nhật ﴾H2﴿ :
3 x 2 = 6m2
Diện tích hình chữ nhật ﴾H1﴿ :
﴾42 – 6 ﴿ : 2 = 18 m2
Chiều rộng hình chữ nhật ban đầu :
18 : 3 = 6m
Chiều dài hình chữ nhật ban đầu :
6 + 5 = 11m
Vậy diện tích thửa đất lúc ban đầu :
6 x 11 = 66 m2
16 tháng 2 2021
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của thửa ruộng đó(Điều kiện: a>0; b>0; \(a\ge b\))
Vì chiều dài lớn hơn chiều rộng 5m nên ta có phương trình: \(a-b=5\)(1)
Diện tích ban đầu của thửa ruộng là: \(a\cdot b\left(m^2\right)\)
Vì khi giảm chiều dài đi 5m và giảm chiều rộng đi 4m thì diện tích mảnh đất giảm đi \(180m^2\)nên ta có phương trình:
\(\left(a-5\right)\left(b-4\right)=ab-180\)
\(\Leftrightarrow ab-4a-5b+20-ab+180=0\)
\(\Leftrightarrow-4a-5b+200=0\)
\(\Leftrightarrow-4a-5b=-200\)
\(\Leftrightarrow4a+5b=200\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a-b=5\\4a+5b=200\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4a-4b=20\\4a+5b=200\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-9b=-180\\a-b=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=20\\a=5+b=5+20=25\end{matrix}\right.\)(thỏa ĐK)
Diện tích của thửa ruộng đó là:
\(S=a\cdot b=25\cdot20=500\left(m^2\right)\)
16 tháng 2 2021
Gọi chiều dài của thửa ruộng là x chiều rộng của thủa ruộng là y (điều kiện :x>y>5)Chiều dài lớn hơn chiều rộng 5m nên ta có phương trình : x-y=5 (1)Nếu chiều rộng giảm đi 4m ,chiều dài giảm đi 5 m thì diện tích giảm đi 180m^2 nên ta có phương trình: ( x-5)(y-4)=xy-180 <=>xy -4x-5y+20=xy-180<=>-4x-5y=-200 (2)tỪ (1),(2) TA CÓ HỆ PHƯƠNG TRÌNH : x-y=5 và -4x-5y=-200=> x=25,y=20 (thỏa mãn điều kiện)Vậy chiều dài thửa ruộng là 25 mchiều rộng thửa ruộng là 20 m
30 tháng 5 2018
Ta chia phần diện tích bị mất đi thành 3 hình chữ nhật A,B,C như hình vẽ.
Diện tích hình C là:
3x 5 = 15( m2)
Vì diện tích hình A và B bằng nhau ( cùng là tích của chiều rộng và 3m) nên diện tích mỗi hình là:
( 42 - 15 ) :2 = 13,5 ( m2)
Chiều rộng thửa đất ban đầu:
13,5 : 3 = 4,5 ( m)
Chiều dài thửa đất ban đầu:
4,5 + 5 = 9,5 ( m)
Diện tích thửa đất ban đầu:
4,5 x 9,5 = 42,75 ( m2)
Đáp số: 42,75 m2
8 tháng 4 2018
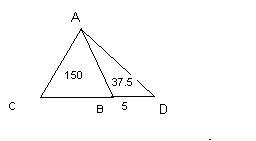
Diện tích ABD = BD x AH : 2
vậy AH = 37,5 x 2 : 5 = 15
vậy Sabc = 150cm2
BC = 150 x2 : 15 =20
MN
5 tháng 2 2021
Gọi: chiều dài ban đầu : 3a (m) , chiều rộng ban đầu : a (m)
Nếu tăng chiều rộng thêm 3m và giảm chiều dài đi 5m thì chiều dài vẫn hơn chiều rộng 20m :
( 3a - 5 ) - ( a+ 3 ) = 20
=> a = 14
Diện tích thửa ruộng :
S = 14 x 3 x 14 = 588 (m2)
5 tháng 2 2021
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của thửa ruộng(Điều kiện: a>0; b>0; \(a\ge b\))
Vì chiều dài gấp ba lần chiều rộng nên ta có phương trình: a=3b(1)
Vì khi tăng chiều rộng thêm 3m và giảm chiều dài đi 5m thì chiều dài vẫn hơn chiều rộng là 20m nên ta có phương trình:
\(\left(a-5\right)-\left(b+3\right)=20\)
\(\Leftrightarrow a-5-b-3-20=0\)
\(\Leftrightarrow a-b-28=0\)
\(\Leftrightarrow a-b=28\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a=3b\\a-b=28\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a-3b=0\\a-b=28\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2b=-28\\a-3b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=14\\a=3\cdot14=42\end{matrix}\right.\)(thỏa ĐK)
Vậy: Chiều dài và chiều rộng của thửa ruộng lần lượt là 42m và 14m
Diện tích thửa ruộng là: \(42\cdot14=588\left(m^2\right)\)
5 tháng 2 2021
Gọi chiều dài thửa ruộng là \(x( m) (x>5)\)
Gọi chiều rộng thửa ruongj là \(y ( m) (y >0)\)
Theo điều kiện đầu ta có phương trình \(x - 3y =0\)(1)
Theo điều kiện sau ta có phương trình \((x-5)-(y+3) =20 \)
⇒ \(x-5-y-3=20\)
⇔\(x-y=28\)(2)
Từ 1 và 2 ta có hệ \(\left\{{}\begin{matrix}x-3y=0\\x-y=28\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=42\left(tm\right)\\y=14\left(tm\right)\end{matrix}\right.\)
⇒ Diện tích thửa ruộng là 14.42=588(m2 )
1 tháng 5 2018
Gọi chiều dài hình chữ nhật là a
Chiều rộng hình chữ nhật là b
Theo bài ra , ta có:
Nếu tăng chiều dài lên 2 m, chiều rộng lên 3 m thì diện tích tăng 100m2:
\(\Rightarrow\)(a + 2) x ( b + 2) = a x b + 100
\(\Rightarrow\) a x b + 3 x a + 2 x b + 6 = a x b + 100
\(\Rightarrow\) a x b + 3 x a + 2 x b - a x b = 100 - 6
\(\Rightarrow\) 3 x a + 2 x b = 94 (1)
Nếu giảm chiều dài và chiều rộng đi 2 m thì diện tích giảm 68 m 2
\(\Rightarrow\)( a - 2) x ( b - 2) = a x b - 68
\(\Rightarrow\)a x b - 2 x a - 2 x b + 4 = a x b - 68
\(\Rightarrow\)a x b - 2 x a - 2 x b - a x b = -68 - 4
\(\Rightarrow\)-2 x a - 2 x b = -72
\(\Rightarrow\)-2 x ( a + b) = - 72
\(\Rightarrow\)a + b = -72 : (-2 )
\(\Rightarrow\)a + b = 36 (2)
Từ (1) và (2) ta có:
3a + 2 b = 94
a + b = 36
\(\Rightarrow\)3a + 2b = 94
2a + 2b = 72
\(\Rightarrow\)a = 94 - 72 = 22
3a +2b = 94
3a + 3b =108
\(\Rightarrow\)b = 14
Diện tích hình chữ nhật là:
14 x 22= 308 ( m2)