Giúp mik với phương trình tích nha mn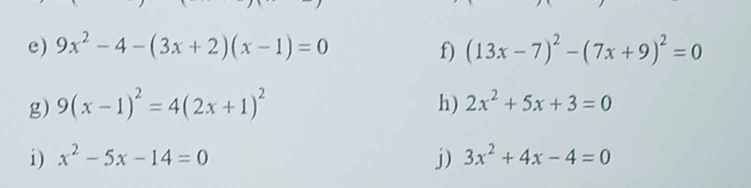
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Mg + 2HCl -> MgCl2 + H2
b) nMg = 4,8/24 = 0,2(mol)
=>nH2 = nMg = 0,2 ( mol )
=> Vdd H2 cần dùng = 0,2/4 = 0,05 (l) = 50ml
c) Theo PT ta có: nHCl = 2nMg = 2.0,2 = 0,4(mol)
=> Vdd HCl cần dùng = 0,4/2 = 0,2(l) = 200(ml)
chắc vậy chứ mình không biết đúng hay không nữa

ĐKXĐ: \(x\notin\left\{0;-1\right\}\)
Ta có: \(\dfrac{1}{x^2}+\dfrac{1}{\left(x+1\right)^2}=15\)
\(\Leftrightarrow\left(\dfrac{1}{x}\right)^2+\left(\dfrac{1}{x+1}\right)^2=15\)
\(\Leftrightarrow\left(\dfrac{1}{x}\right)^2+\left(\dfrac{1}{x+1}\right)^2-\dfrac{2}{x\left(x+1\right)}+\dfrac{2}{x\left(x+1\right)}=15\)
\(\Leftrightarrow\left(\dfrac{1}{x}-\dfrac{1}{x+1}\right)^2+\dfrac{2}{x\left(x+1\right)}=15\)
\(\Leftrightarrow\left(\dfrac{x+1}{x\left(x+1\right)}-\dfrac{x}{x\left(x+1\right)}\right)^2+\dfrac{2}{x\left(x+1\right)}=15\)
\(\Leftrightarrow\left(\dfrac{1}{x\left(x+1\right)}\right)^2+\dfrac{2}{x\left(x+1\right)}=15\)
\(\Leftrightarrow\dfrac{1}{x^2\cdot\left(x+1\right)^2}+\dfrac{2}{x\left(x+1\right)}-15=0\)(1)
Đặt \(\dfrac{1}{x\left(x+1\right)}=a\)(Điều kiện: \(x\notin\left\{0;-1\right\}\)
(1)\(\Leftrightarrow a^2+2a-15=0\)
\(\Leftrightarrow a^2+5a-3a-15=0\)
\(\Leftrightarrow a\left(a+5\right)-3\left(a+5\right)=0\)
\(\Leftrightarrow\left(a+5\right)\left(a-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+5=0\\a-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-5\\a=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{x\left(x+1\right)}=-5\\\dfrac{1}{x\left(x+1\right)}=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\left(x+1\right)=-\dfrac{1}{5}\\x\left(x+1\right)=\dfrac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+x+\dfrac{1}{5}=0\\x^2+x-\dfrac{1}{3}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{20}=0\\x^2+2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{7}{12}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{20}\\\left(x+\dfrac{1}{2}\right)^2=\dfrac{7}{12}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=\dfrac{\sqrt{5}}{10}\\x+\dfrac{1}{2}=-\dfrac{\sqrt{5}}{10}\\x+\dfrac{1}{2}=\dfrac{\sqrt{21}}{6}\\x+\dfrac{1}{2}=-\dfrac{\sqrt{21}}{6}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-5+\sqrt{5}}{10}\left(nhận\right)\\x=\dfrac{-5-\sqrt{5}}{10}\left(nhận\right)\\x=\dfrac{-3+\sqrt{21}}{6}\left(nhận\right)\\x=\dfrac{-3-\sqrt{21}}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{-5+\sqrt{5}}{10};\dfrac{-5-\sqrt{5}}{10};\dfrac{-3+\sqrt{21}}{6};\dfrac{-3-\sqrt{21}}{6}\right\}\)


Ta có: \(\sqrt{16x}=8\)
\(\Leftrightarrow16x=64\)
hay x=4

Tham khảo
Người ta phải trồng cây đúng thời vụ là vì: các loại cây khác nhau có nhu cầu khác nhau về các điều kiện ngoại cảnh. Cho nên, muốn cho cây sinh trưởng, phát triển tốt thì phải trồng cây vào thời điểm có khí hậu, thời tiết phù hợp nhất đổi với cây. Có như vậy cây mới sử dụng được các yếu tố ánh sáng, nhiệt độ, độ ẩm... của môi trường phù hợp nhất và hiệu quả nhất.

Gọi thời gian của T,D,M lần lượt là \(a,b,c(giờ;a,b,c>0)\)
Áp dụng tc dtsbn:
\(10a=9b=8c\Leftrightarrow\dfrac{10a}{360}=\dfrac{9b}{360}=\dfrac{8c}{360}\Leftrightarrow\dfrac{a}{36}=\dfrac{b}{40}=\dfrac{c}{45}=\dfrac{c-a}{45-36}=\dfrac{0,3}{9}=\dfrac{1}{30}\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{6}{5}\\b=\dfrac{4}{3}\\c=\dfrac{3}{2}\end{matrix}\right.\)
Vậy ...

Gọi x là qđ AB (km)
Vận tốc đi là \(25\left(\dfrac{km}{h}\right)\)
Vận tốc về là \(30\left(\dfrac{km}{h}\right)\)
Thời gian đi là \(\dfrac{x}{25}\left(h\right)\)
Thời gian về là \(\dfrac{x}{30}\left(h\right)\)
20p = 1/3(h)
Do thời gian về ít hơn lúc đi là 20p nên ta có
\(\dfrac{x}{25}-\dfrac{x}{30}=\dfrac{1}{3}\\ \Leftrightarrow30x-25x=\dfrac{1}{3}\\ \Leftrightarrow5x=\dfrac{1}{3}\\ \Leftrightarrow x=15\)
Cách giải đây nhé!
Gọi thời gian lúc đi là x(x>0) (h)
Đổi 20 phút = 1/3 giờ
Do thời gian về ít hơn thời gian đi là 20 phút nên thời gian lúc về là x−1/3
Do quãng đường không đổi nên ta có phương trình :
25x= 30(x−1/3)
⇔ 25x= 30x−10
⇔ −5x= −10
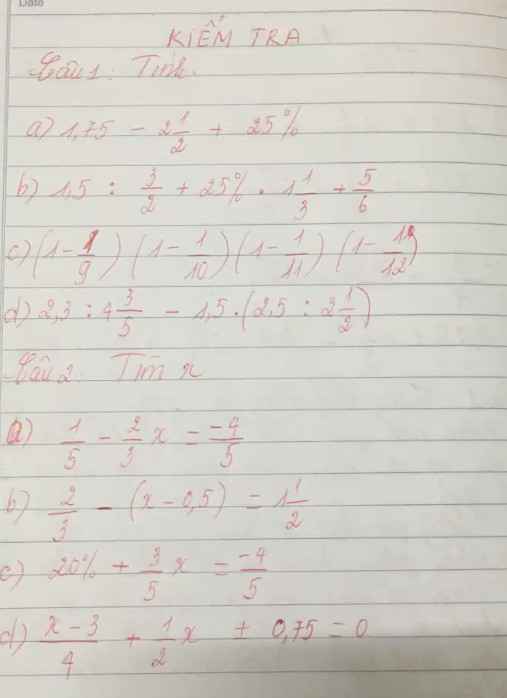
 mn giúp mik vs mik cần gấp( có trình bày nha~)
mn giúp mik vs mik cần gấp( có trình bày nha~)
e.\(\Leftrightarrow9x^2-4-\left(3x^2-x-2\right)=0\)
\(\Leftrightarrow9x^2-4-3x^2+x+2=0\)
\(\Leftrightarrow6x^2+x-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
f.\(\Leftrightarrow\left(13x-7\right)^2=\left(7x+9\right)^2\)
\(\Leftrightarrow13x-7=7x+9\)
\(\Leftrightarrow6x=16\Leftrightarrow x=\dfrac{16}{6}\)
g.\(\Leftrightarrow\left(9x-9\right)^2=\left(8x+4\right)^2\)
\(\Leftrightarrow9x-9=8x+4\)
\(\Leftrightarrow x=13\)
h.\(\Leftrightarrow2x^2+2x+3x+3=0\)
\(\Leftrightarrow2x\left(x+1\right)+3\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
i,\(\Leftrightarrow x^2+2x-7x-14=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=7\end{matrix}\right.\)
j.\(\Leftrightarrow\left(x-\dfrac{2}{3}\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-2\end{matrix}\right.\)