Tính tổng: A = 3 + 32 + 33 + 34 +...+ 320
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
1
NN
14 tháng 8 2023
1.
a.\(A=1+2^1+2^2+2^3+...+2^{2007}\)
\(2A=2+2^2+2^3+....+2^{2008}\)
b. \(A=\left(2+2^2+2^3+...+2^{2008}\right)-\left(1+2^1+2^2+..+2^{2007}\right)\)
\(=2^{2008}-1\) (bạn xem lại đề)
2.
\(A=1+3+3^1+3^2+...+3^7\)
a. \(2A=2+2.3+2.3^2+...+2.3^7\)
b.\(3A=3+3^2+3^3+...+3^8\)
\(2A=3^8-1\)
\(=>A=\dfrac{2^8-1}{2}\)
3
.\(B=1+3+3^2+..+3^{2006}\)
a. \(3B=3+3^2+3^3+...+3^{2007}\)
b. \(3B-B=2^{2007}-1\)
\(B=\dfrac{2^{2007}-1}{2}\)
4.
Sửa: \(C=1+4+4^2+4^3+4^4+4^5+4^6\)
a.\(4C=4+4^2+4^3+4^4+4^5+4^6+4^7\)
b.\(4C-C=4^7-1\)
\(C=\dfrac{4^7-1}{3}\)
5.
\(S=1+2+2^2+2^3+...+2^{2017}\)
\(2S=2+2^2+2^3+2^4+...+2^{2018}\)
\(S=2^{2018}-1\)
14 tháng 8 2023
4:
a:Sửa đề: C=1+4+4^2+4^3+4^4+4^5+4^6
=>4*C=4+4^2+...+4^7
b: 4*C=4+4^2+...+4^7
C=1+4+...+4^6
=>3C=4^7-1
=>\(C=\dfrac{4^7-1}{3}\)
5:
2S=2+2^2+2^3+...+2^2018
=>2S-S=2^2018-1
=>S=2^2018-1
PT
1
22 tháng 8 2021
Ta có: \(A=3+3^2+3^3+...+3^{20}\)
\(\Leftrightarrow3\cdot A=3^2+3^3+3^4+...+3^{21}\)
\(\Leftrightarrow2\cdot A=3^{21}-3\)
hay \(A=\dfrac{3^{21}-3}{2}\)
NT
0
KJ
1
Q
13 tháng 12 2021
Tham khảo
Ta có: 3A = 3.(1+3+32+33+...+399+3100)(1+3+32+33+...+399+3100)
3A = 3+32+33+...+3100+31013+32+33+...+3100+3101
Suy ra: 3A – A = (3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)(3+32+33+...+3100+3101)−(1+3+32+33+...+399+3100)
2A = 3101−13101−1
⇒⇒ A = 3101−123101−12
Vậy A = 3101−12
KJ
2
16 tháng 12 2021
\(A=1-3+3^2-3^3+3^4-...-3^{98}-3^{99}+3^{100}\\ 3A=3-3^2+3^3-3^4-...-3^{98}+3^{99}-3^{100}+3^{101}\\ 3A-A=3^{101}-1\\ \Rightarrow A=\dfrac{3^{101}-1}{2}\)
PM
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
24 tháng 12 2023
A = 1 + 3 + 32 + 33 + 34 + ... + 32022
3A = 3 + 32 + 33 + ... + 34 + ... + 32022 + 32023
3A - A = (3 + 32 + 33 + ... + 34 + 32022 + 32023) - (1 + 3+...+ 32022)
2A = 3 + 32 + 33 + 34 + ... + 32022 + 32023 - 1 - 3 - ... - 32022
2A = (3 - 3) + (32 - 32) + (34 - 34) + (32022 - 32022) + (32023 - 1)
2A = 32023 - 1
A = \(\dfrac{3^{2023}-1}{2}\)
A = \(\dfrac{3^{2023}}{2}\) - \(\dfrac{1}{2}\)
B - A = \(\dfrac{3^{2023}}{2}\) - (\(\dfrac{3^{2023}}{2}\) - \(\dfrac{1}{2}\))
B - A = \(\dfrac{3^{2023}}{2}\) - \(\dfrac{3^{2023}}{2}\) + \(\dfrac{1}{2}\)
B - A = \(\dfrac{1}{2}\)
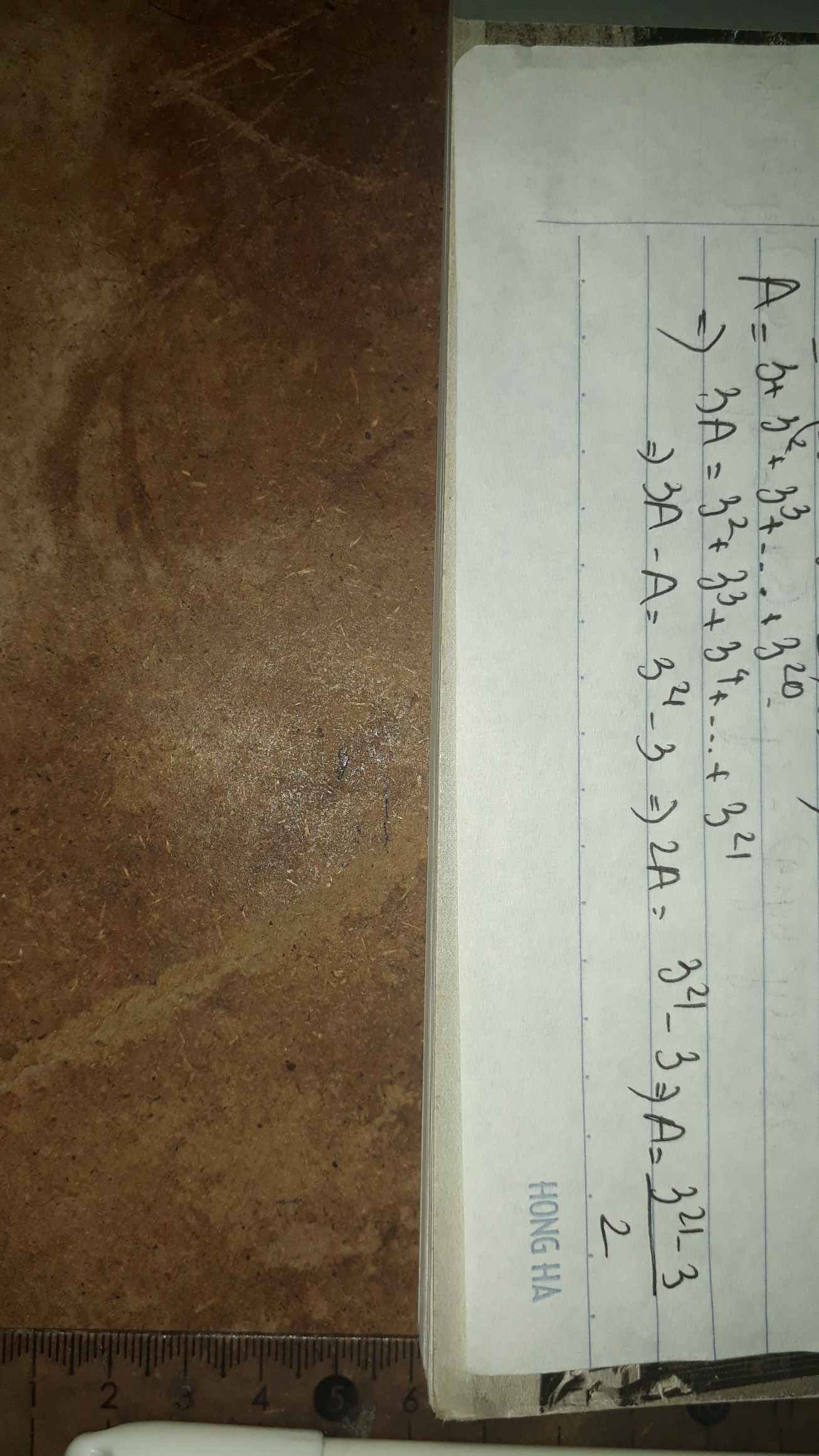
\(A=3+3^2+3^3+3^4+...+3^{20}\)
\(3A=3^2+3^3+3^4+3^5+...+3^{21}\)
\(3A-A=3^{21}-3\)
(Bạn komhieeur chỗ nào thì cứ hỏi mink nhé)