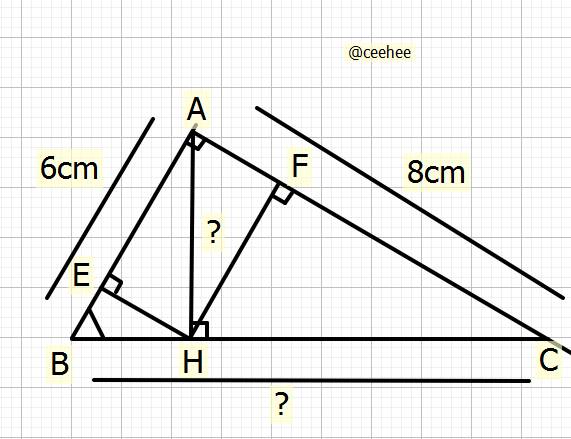
Cho tam giác ABC vuông tại A. Đường phân giác góc C cắt cạnh AB tại I. Gọi E, F lần lượt là hình chiếu của A, B trên đường thẳng CI. = 6cm, AC = 8cm, đường cao AH.
a) Cm CE.CB = CF.CA
b) Cm
c) Kẻ đường cao AD của DABC. Cm DABC đồng dạng DDBA.. C/m: AC2 = CD.CB