a3+6= -3a-2a2. Tính giá trị A=a-1/a+3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Gợi ý: a 2 − 5 a + 4 = ( a − 1 ) ( a − 4 ) ; a 2 + 3 a − 4 = ( a − 1 ) ( a + 4 )
Ta rút gọn được A = a + 1 a − 4
b) Thay a = 5 vào biểu thức A tìm được A = 6
c) Ta biến đổi A = a + 1 a − 4 = 1 + 5 a − 4
⇒ A ∈ ℤ ⇒ a ∈ − 1 ; 3 ; 5 ; 9

Ta có
f ' x = 2 a 2 - 3 cos x + 4 a cos 2 x f " x = 2 3 - a 2 sin x + 8 a sin 2 x
Hàm số f(x) đạt cực tiểu tại x = π 3 khi và chỉ khi
f ' π 3 = 0 f " π 3 > 0 ⇔ a 2 - 2 a + 3 = 0 - 3 a 2 - 4 a - 3 > 0 ⇔ a = 1
Đáp án B


Xét hiệu \(2a^2+2b^2-\left(a^3+ab^2\right)=\left(2a^2-a^3\right)+\left(2b^2-ab^2\right)\)
\(=a^2\left(2-a\right)+b^2\left(2-a\right)\)
\(=\left(a^2+b^2\right)\left(2-a\right)\)
Do \(a^2+b^2\ge0;\forall a;b\) nên:
\(2a^2+2b^2>a^3+ab^2\) khi \(\left\{{}\begin{matrix}a^2+b^2\ne0\\2-a>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a^2+b^2\ne0\\a< 2\end{matrix}\right.\)
\(2a^2+2b^2=a^3+ab^2\) khi \(\left[{}\begin{matrix}a^2+b^2=0\\2-a=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a=b=0\\a=2\end{matrix}\right.\)
\(2a^2+2b^2< a^3+ab^2\) khi \(\left\{{}\begin{matrix}a^2+b^2\ne0\\a>2\end{matrix}\right.\) \(\Rightarrow a>2\)
\(2a^2+2b^2\ge a^3+ab^2\) khi \(2-a\ge0\Leftrightarrow a\le2\)

\(a^3+6=-3a-2a^2\)
\(\Leftrightarrow a^3+2a^2+6+3a=0\)
\(\Leftrightarrow a^2\left(a+2\right)+3\left(a+2\right)=0\)
\(\Leftrightarrow\left(a+2\right)\left(a^2+3\right)=0\)
\(\Leftrightarrow a+2=0\left(do.a^2+3>0\right)\)
<=>a=-2
thay a=-2 vào biểu thức ta được \(A=\frac{-2-1}{-2+3}=\frac{-3}{1}=-3\)
Ta có : a3+6=-3a-2a2
<=> a3+6+3a+2a2=0
<=>(a3+2a2)+(3a+6)=0
<=>a2(a+2)+3(a+2)=0
<=>(a2+3)(a+2)=0
\(\hept{\begin{cases}a^2+3=0\\a+2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a^2=-3\\a=-2\end{cases}\Leftrightarrow}\hept{\begin{cases}a\in\varnothing\\a=-2\end{cases}}}\)
Thay a=-2 vào biểu thức :
=> A= \(\frac{-2-2}{-2+3}=\frac{-4}{1}=-4\)

a) Ta có x 6 + 2 x 3 + 3 x 3 − 1 . 3 x x + 1 . x 2 + x + 1 x 6 + 2 x 3 + 3 = 3 x x 2 − 1
b) Gợi ý: a 3 + 2 a 2 - a - 2 = (a - 1)(a + 1) (a + 2)
Thực hiện phép tính từ trái qua phải thu được: = 1 3

A= a^3 + 3a^2 + 3a +6
=a3+3a2+3a+1+5
=(a+1)3+5
thay a=29 vào (a+1)3+5 ta được:
(29+1)3+5=303+5=27005
Vậy với x=29 thì A=27005
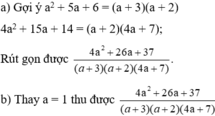
a3+6= -3a-2a2.
->a=-2
\(\Leftrightarrow A=\frac{-2-1}{-2+3}=\frac{-3}{1}=-3\)
vậy A=-3
ĐKXD: a+3 khác 0 => a khác -3
Ta có a^3+6+3a+2a^2=0
<=> a^2(a+2) + 3(a+2)=0
<=> (a+2)(a^2+3)=0
=> a+2=0 <=> a= -2
Suy ra
a-1/a+3= -2-1/-2+3=-3/1=-3