Cho tam giác ABC nhọn có điểm M di động trong tam giác. Gọi D,E,F lần lượt là hình chiếu của M lên BC, CA, AB. Tìm vị trí của điểm M để \(MD\times ME\times MF\) lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 3 2016
Tứ giác BEMF là hình bình hành ( hai cặp cạnh đối song song) |
Kẻ AH vuông góc BC tại H , AH cắt MF tại G. Ta có diện tích ABC=1/2AH*BC và S bemf=fm*gh nên Sbemf/Sabc=2*HG/AH*FM/BC |
Gọi AM = x; MC = y thìAC = x + y Xét tam giácABC có MF // BC (gt)FM/BC=AM/AC ( hệ quả định lí Talet) Thì FM/BC=x/x+y |
Xét tam giácAHC có GM //HCthì HG/AH=CM/AC ( định lí Talet) HG/AH=x/x+y |
Do đó Sbefm/Sabc=2*xy/(x+y)^2 Ta có : (x-y)^2>=0thif(x+y)^2>=4xy thì xy/(x+y)^2<=1/4 |
Sbemf/Sabc<=2*1/4hay Sbemf<=1/2Sabc |
Mà Sabc không đổi nên Sbemf đạt giá trị lớn nhất là 1/2Sabc khi và chỉ khi x=y Hay M là trung điểm của AC. Gõ mỏi tay ko biết đc j ko-_- |
CM
28 tháng 5 2019
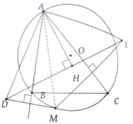
Kẻ AH ⊥ DE tại H
D A E ^ = 2 B A C ^
=> D A H ^ = B A C ^
Từ DE=2DH; AD=AM=AE
Suy ra DH=AD.sin D A H ^
Từ đó D E m a x <=> AM = 2R
12 tháng 2 2016
a)tứ giác AEDF là hình chữ nhật (vì E=A=F=900 )
Để tứ giác AEDF là hình vuông thì AD là tia phân giác của góc BAC
b)do tứ giác AEDF là hình chữ nhật nên AD=EF
=>3AD+4EF nhỏ nhất => AD nhỏ nhất
D là hình chiếu góc vuông của A lên BC
18 tháng 8 2023
a: Xét tứ giác ADME có
gócADM=góc AEM=góc DAE=90 độ
=>ADME là hình chữ nhật
b: góc AHM=góc AEM=góc ADM=90 độ
=>A,D,H,M,E cùng thuộc đường tròn đường kính AM
mà ED và AM cùng là đường kính của đường tròn đường kính AM(ED=AM)
nên H nằm trên đường tròn đường kính DE
=>góc DHE=90 độ
c: DE=AM
AM>=AH
=>DE>=AH
Dấu = xảy ra khi M trùng với H
=>M là chân đường cao kẻ từ A xuống BC