un…...erline
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 8 2023
Viết lại đề: \(\left\{{}\begin{matrix}u_1=\dfrac{1}{7}\\u_{n+1}=\dfrac{u_n\left(1-u_n^8\right)}{1+u_n}\end{matrix}\right.\)
*Tính \(\lim\limits_{n\rightarrow+\infty}u_n\):
Bằng quy nạp, dễ chứng minh được \(0< u_n< 1,\forall n=1,2,...\)
Ta có \(u_{n+1}-u_n=\dfrac{-u_n^9-u_n^2}{1+u_n}< 0\) nên \(\left(u_n\right)\) là dãy giảm. Mà \(\left(u_n\right)\) bị chặn nên \(\left(u_n\right)\) có giới hạn hữu hạn.
Đặt \(\lim\limits_{n\rightarrow+\infty}u_n=L\left(0\le L< 1\right)\) thì \(L=\dfrac{L\left(1-L^8\right)}{1+L}\)
\(\Leftrightarrow\left[{}\begin{matrix}L=0\\\dfrac{1-L^8}{1+L}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}L=0\\1-L^8=1+L\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}L=0\\L=-1\end{matrix}\right.\)
\(\Rightarrow L=0\) \(\Rightarrow\lim\limits_{n\rightarrow+\infty}u_n=0\)
AH
Akai Haruma
Giáo viên
28 tháng 3 2021
Lời giải:
$\frac{u_{n-1}}{u_n}=\frac{n^2}{n^2-1}>0$ với mọi $n\geq 2$ nên $u_{n-1}, u_n$ luôn cùng dấu.
Mà $u_1=2017>0$ nên $u_n>0$ với mọi $n=1,2,...$
Mặt khác:
$n^2(u_{n-1}-u_n)=u_{n-1}>0\Rightarrow u_{n-1}>u_n$ nên dãy $(u_n)$ là dãy giảm.
Dãy giảm và bị chặn dưới nên $u_n$ hội tụ. Đặt $\lim u_n=a$.
Ta có: $a=n^2(a-a)\Rightarrow a=0$
Vậy $\lim u_n=0$
CM
26 tháng 4 2018
Chọn C
1. u n = 3 n + 1 2. u n = 4 − 5 n
3. u n = 2 n + 3 5 4. u n = n + 1 n
* Xét dãy số: u n = 3 n + 1
Ta có:
u n + 1 − u n = 3 ( n + 1 ) + 1 − 3 n − 1 = 3
Dãy số này là cấp số cộng có công sai d= 3.
* Xét dãy số u n = 4 − 5 n .
Ta có:
u n + 1 − u n = 4 − 5 ( n + 1 ) − ( 4 − 5 n ) = − 5
Dãy số này là cấp số cộng có công sai d = -5
* Xét dãy số u n = 2 n + 3 5
Ta có:
u n + 1 − u n = 2 ( n + 1 ) + 3 5 − 2 n + 3 5 = 2 5 .
Dãy (un) là cấp số cộng có công sai d = 2 5
* Xét dãy số u n = n + 1 n
Ta có:
u n + 1 − u n = n + 1 + 1 n + 1 − n + 1 n = ( n + 2 ) . n − ( n + 1 ) 2 n . ( n + 1 ) = − 1 n ( n + 1 ) ⇒ ( u n )
không là cấp số cộng
CM
28 tháng 6 2018
Chọn C.
Chứng minh bằng phương pháp quy nạp toán học ta có n ≤ 2n, ∀n ∈ N
Nên ta có :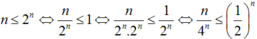 
Suy ra :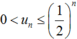 
mà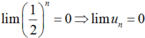 
.
CM
19 tháng 2 2018
a)u(n+1) = 1 + 1/(n+1); v(n+1) = 5(n + 1) - 1 = 5n + 4
b) Ta có:
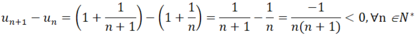
⇒ u(n+1) < un, ∀n ∈ N*
v(n+1) - vn = (5n + 4) - (5n - 1) = 5 > 0
⇒ v(n+1) > vn ,∀n ∈ N*
underline
der