Cho ABC có AB < AC. Tia AD là tia phân giác của góc A (D thuộc BC) . Trên
cạnh AC lấy E sao cho AB = AE. Đường thẳng DE cắt đường thẳng AB tại I.
Chứng minh:
a,tam giác ABD = AED
b, AI = AC
c, Đường thẳng AD vuông góc với đoạn thẳng IC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2023
Xet ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
=>ΔABC=ΔADE
=>BC=DE
12 tháng 4 2022
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
b: Ta có: ΔABD=ΔAED
nên DB=DE
mà DE<DC
nên DB<DC
c: Ta có: AB=AE
DB=DE
Do đó: AD là đường trung trực của BE
30 tháng 11 2021
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
5 tháng 6 2023
a: Xét ΔBAE và ΔBDE có
BA=BD
góc ABE=góc DBE
BE chung
=>ΔBAE=ΔBDE
=>AE=DE
b: Xét ΔEAI vuông tại A và ΔEDC vuông tại D có
EA=ED
góc AEI=góc DEC
=>ΔEAI=ΔEDC
c: BI=BC
EI=EC
=>BE là trung trực của CI
=>BE vuông góc CI
20 tháng 4 2019
Xin lỗi mk ko biết vẽ hình trên máy
a) Xét tam giác ABD và tan giác EBD có :
BD chung
góc ABD = góc EBD ( vì BD la phân giác góc B )
góc A = góc E ( = 90 )
=> Tam giác ABD = tam giác EBD ( cạnh huyền- góc nhọn )
=> AD = DE
Chúc bạn hc tốt
KV
18 tháng 12 2022
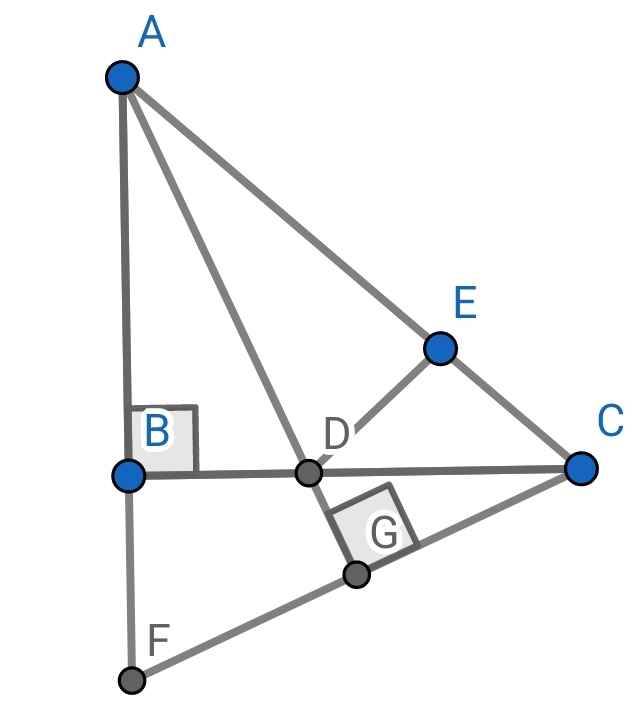
a) Xét ∆ADB và ∆ADE có:
AD chung
Góc BAD = góc EAD (AD là tia phân giác của góc BAC)
AB = AE (gt)
⇒∆ADB = ∆ADE (c-g-c)
b) Do ∆ADB = ∆ADE (c-g-c)
⇒góc ABD = góc AED (hai góc tương ứng)
⇒góc AED = 90⁰
Hay DE vuông góc AC
c) Gọi G là giao điểm của CF và AD
Do góc BAD = góc EAD (cmt)
⇒góc FAG = góc CAG
Xét hai tam giác vuông: ∆AGF và ∆AGC có:
AG chung
góc FAG = góc CAG (cmt)
⇒∆AGF = ∆AGC (cạnh góc vuông - góc nhọn kề)
⇒AF = AC (hai cạnh tương ứng)
Mà AF = AB + BF
AC = AE + EC
AB = AE
⇒BF = CE
TL
26 tháng 4 2018
a, Xét tam giác DAE và tam giác BAC có
DAE = BAC ( đối đỉnh )
AD = AB ( gt)
AE= AC ( gt)
=> tam giác DAE = tam giác BAC
=> BC= DE
b, ta có DAE = BAC = 90 độ ( 2 góc đối đỉnh )
lại có BAD = CAE đối đỉnh
=> BAD=CAE = 360 - (BaC + DAE) tất cả trên 2
<=> BAD= 360 -180 tâts cả trên 2
<=> BAD = 180 trên 2
<=> BAD = 90 độ
=> tam giác BAD vuông lại A
mà AB =AD (gt)
=> BAD vuông cân
=> DBA = BDA = 90 trên 2 = 45 độ
Chứng mình tương tự tam giác CAE vuông cân
=>AEC=ACE= 90 trên 2 = 45 độ
=> DBA=AEC=45 độ
mà chúng ở vị trí sole trong
=> BD // CE
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED