Điểm I nằm trên đoạn thẳng BC và 3IB=2IC. Vậy BC/IC
giúp với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3IB = 2TC
IB/2 = IC/3 = TB + IC/ 2+3 = BC/5
TC/3 = BC/5 = BC/IC = 5/3
Bn bảng A hay bảng B thế???

Có :
\(IB=IC=BC\)
\(3IB=2IC\)
\(\Rightarrow\frac{IB}{2}=\frac{IC}{3}\)
Đặt \(\frac{IB}{2}=\frac{IC}{3}=k\Rightarrow IC=3k\)
\(IB=2k\)
\(BC=3k+2k=5k\)
\(\Rightarrow\frac{BC}{IC}=\frac{5k}{3k}=\frac{5}{3}\)

* ta có 3IB=2IC =>\(\dfrac{IB}{2}=\dfrac{IC}{3}\)
Vì I nằm trên đoạn thẳng BC =>\(\dfrac{IB}{2}=\dfrac{IC}{3}=\dfrac{IB+IC}{2+3}=\dfrac{BC}{5}\)
*\(\dfrac{IC}{3}=\dfrac{BC}{5}\)=>\(\dfrac{BC}{IC}=\dfrac{5}{3}\)

3IB=2IC
nên IB=2/3IC
IB+IC=BC
=>2/3IC+IC=BC
=>5/3IC=BC
=>5IC=3BC
=>BC/IC=5/3


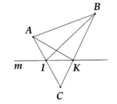
a) Vì hai điểm A, B nằm trên hai nửa mặt phẳng đối nhau bờ m nên đoạn thẳng AB cắt đường thẳng m.
b) Từ câu a), ta suy ra điểm K nằm giữa hai điểm B, C nên tia AK nằm giữa hai tia AB và AC.
Tương tự, ta có điểm I nằm giữa hai điểm A, C nên tia BI nằm giữa, hai tia BA, BC.
c*) Từ câu b), ta suy ra tia BI nằm giữa hai tia BA,BK nên tia BI cắt đoạn thẳng AK tại một điểm nằm giữa A và K.
Lập luận tương tự, ta có tia AK cắt đoạn thẳng BI tại một điểm nằm giữa B và I. Từ đó suy ra hai đoạn thẳng AK và BI cắt nhau.

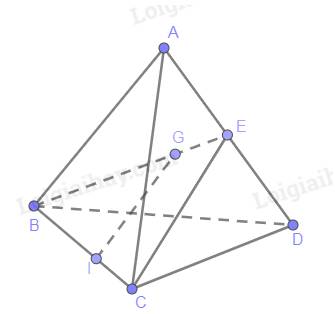
Tam giác BCE có E là trung điểm AD
Suy ra:\(\frac{{BG}}{{BE}} = \frac{{BI}}{{BC}} = \frac{2}{3}\)
Theo Ta lét, IG //CE
Mà CE thuộc (ACD)
Suy ra: IG // (ACD)

1, Trên đoạn thẳng BC, có:
I là trung điểm của BC
IB=IC=BC\2=6\2=3 (cm)
2,? vì bạn ko nói cách điểm B,C hay I.
Vì I E BC=>IB+IC=BC
Ta có: 3IB=2IC
<=>IB/2=IC/3
theo t/c dãy tỉ số=nhau ta có:
IB/2=IC/3=(IB+IC)/(2+3)=BC/5
=>IC/3=BC/5=>BC/IC=5/3