Với x thuộc tập hợp nào thì nhị thức f(x) = x(x^2 - 1) không âm?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 5 2017
Chọn C
Ta có
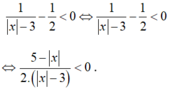
Đặt 
bpt trở thành 
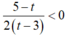
Bảng xét dấu
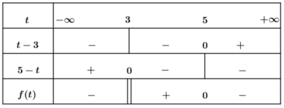
Căn cứ bảng xét dấu ta được
D
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
\(\left|2x-5\right|-3\le0\)
\(\Leftrightarrow\left|2x-5\right|\le3\)
\(\Leftrightarrow-3\le2x-5\le3\)
\(\Leftrightarrow1\le x\le4\)
D
2
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2022
\(\left|2x-5\right|-3\le0\)
\(\Leftrightarrow\left|2x-5\right|\le3\)
\(\Leftrightarrow-3\le2x-5\le3\)
\(\Leftrightarrow1\le x\le4\)
\(\Rightarrow x\in\left[1;4\right]\) (và các tập con của nó)
CM
28 tháng 12 2018
Chọn D.
Để f(x) = x(5x + 2) - x( x 2 + 6) không dương thì
x(5x + 2) - x(x2 + 6) ≤ 0 ⇔ x( x 2 - 5x + 4) ≥ 0
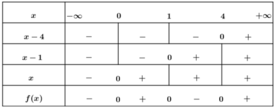
Vậy x ∈ [0;1] ∪ [4; + ∞ ).
22 tháng 8 2019
a) ta có:
+) x = 5 => f(5) = 52 - 6.5 + 5 = 25 - 30 + 5 = 0
=> x = 5 là nghiệm của f(x)
+) x = 3 => f(3) = 32 - 6.3 + 5 = 9 - 18 + 5 = -4
=> x = 3 ko là nghiệm của f(x)
+) x = 1 =. f(1) = 12 - 6.1 + 5 = 1 - 6 + 5 = 0
=> x = 1 là nghiệm của f(x)
+) x = 0 => f(0) = 02 - 6.0 + 5 = 5
=> x = 5 ko là nghiệm của f(x)
b) Tập hợp S = {5; -1}
c) Ta có : x4 \(\ge\)0 ; 1/5x2 \(\ge\)0 ; 2012 > 0
=> x4 + 1/5x2 + 2012 > 0
=> đa thức h(x) ko có nghiệm
22 tháng 8 2019
\(a.\)Thay lần lượt các giá trị của \(x\)trong tập hợp số \(\left\{5;3;-1;0\right\}\)vào đa thức \(f\left(x\right)\)như bn Edogawa Conan nha !
Ta thấy \(f\left(5\right)=5^2-6.5+5=0\)nên \(x=5\)là 1 ngiệm của \(f\left(x\right)\)
\(b.\)Ta có: \(f\left(x\right)=x^2-x-5x+5=x\left(x-1\right)-5\left(x-1\right)=\left(x-1\right)\left(x-5\right)\)
\(f\left(x\right)=0\Leftrightarrow\cdot x-1\left(x-5\right)=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=5\end{cases}}\)
\(c.\)Xét đa thức \(h\left(x\right)=x^4+\frac{1}{5}x^2+2012\)
Do \(x^4\ge0\)và \(\frac{1}{5}x^2\ge0\)với mọi \(x\)nên \(h\left(x\right)>0\)với mọi \(x\)
Vậy \(h\left(x\right)\ne0\)với mọi \(x\)Do đó đa thức \(h\left(x\right)\)không có nghiệm
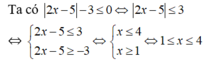
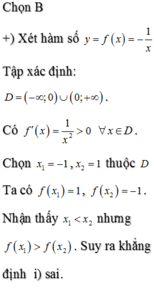
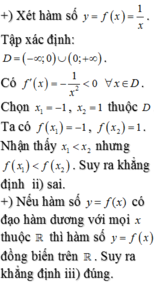
Xét f(x) = \(x\left(x^2-1\right)=x\left(x-1\right)\left(x+1\right)\)
f(x) = 0 khi x = 0 hoặc x = 1 hoặc x = -1
Ta có bảng
x \(-\infty\) -1 0 1 \(+\infty\)
x - | - 0 + | +
x-1 - | - | - 0 +
x+1 - 0 + | + | +
f(x) - 0 + 0 - 0 +
=> f(x) \(\ge0\Leftrightarrow x\in\left[-1;0\right]\cup\left[1;+\infty\right]\)